Tổng bình phương các nghiệm của phương trình 5 3 x − 2 = 1 5 − x 2 bằng
A. 0
B. 5
C. 2
D. 3
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Tìm tổng bình phương các nghiệm của phương trình \(\left(x-1\right)\left(x-3\right)+3\sqrt{x^2-4x+5}-2=0\)
\(\Leftrightarrow x^2-4x+5+3\sqrt{x^2-4x+5}-2=0\)
Đặt \(\sqrt{x^2-4x+5}=t>0\)
\(\Rightarrow t^2+3t-2=0\Rightarrow\left[{}\begin{matrix}t=\dfrac{-3+\sqrt{17}}{2}\\t=\dfrac{-3-\sqrt{17}}{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow x^2-4x+5=\dfrac{13-3\sqrt{17}}{2}\)
\(\Leftrightarrow x^2-4x+\dfrac{-3+3\sqrt{17}}{2}=0\)
\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=4^2-2\left(\dfrac{-3+3\sqrt{17}}{2}\right)=19-3\sqrt{17}\)
Tổng các bình phương các nghiệm của phương trình x − 1 x − 3 + 3 x 2 − 4 x + 5 − 2 = 0 là:
A. 17
B. 4
C. 16
D. 8
Ta có x − 1 x − 3 + 3 x 2 − 4 x + 5 − 2 = 0
⇔ x 2 − 4 x + 5 + 3 x 2 − 4 x + 5 − 4 = 0
⇔ x 2 − 4 x + 5 − 1 x 2 − 4 x + 5 + 4 = 0
⇔ x 2 − 4 x + 5 = 1 x 2 − 4 x + 5 = − 4 ( V N )
⇔ x 2 − 4 x + 5 = 1 ⇔ x 2 − 4 x + 4 = 0 ⇔ x = 2
Vậy tổng bình phương các nghiệm là 2 2 = 4
Đáp án cần chọn là: B
Không giải phương trình \(x^2-11x+5=0\) (1)
a, Tính tổng bình phương các nghiệm của phương trình (1)
b, Lập phương trình bậc 2 có nghiệm là nghịch đảo các nghiệm của phương trình (1)
Cho phương trình: x^2 + 2(m-2)x -(2m-7)=0.Gọi x1,x2 là hai nghiệm của phương trình (1).
Tìm m để phương trình (1) có tổng bình phương (1) có tổng bình phương các nghiệm đạt giá trị nhỏ nhất.
Câu 1: Tìm tất cả các giá trị cuả tham số m để phương trình \(4\sqrt{x^2-4x+5} =x^2-4x+2m-1\) có 4 nghiệm phân biệt
Câu 2: Tìm các giá trị của tham số m sao cho tổng các bình phương hai nghiệm của phương trình \((m-3)x^2+2x-4=0\) bằng 4
Câu 3: Cho tam giác ABC có \(BC=a, AC=b, AB=c\) và I là tâm đường tròn nội tiếp tam giác. Chứng minh rằng: \(a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{0}\)
Câu 4: Cho tam giác ABC. Gọi D,I lần lượt là các điểm xác định bởi \(3\overrightarrow{BD}-\overrightarrow{BC}=\overrightarrow{0}\) và \(\overrightarrow{IA}+\overrightarrow{ID}=\overrightarrow{0}\). Gọi M là điểm thỏa mãn \(\overrightarrow{AM}=x\overrightarrow{AC}\) (x∈R)
a) Biểu thị \(\overrightarrow{BI}\) theo \(\overrightarrow{BA}\) và \(\overrightarrow{BC}\)
b) Tìm x để ba điểm B,I,M thẳng hàng
1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)
3.
Nối AI kéo dài cắt BC tại D thì D là chân đường vuông góc của đỉnh A trên BC
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{AB}{AC}=\dfrac{c}{b}\)
\(\Rightarrow\overrightarrow{BD}=\dfrac{c}{b}\overrightarrow{DC}\)
\(\Leftrightarrow\overrightarrow{ID}-\overrightarrow{IB}=\dfrac{c}{b}\left(\overrightarrow{IC}-\overrightarrow{ID}\right)\)
\(\Leftrightarrow b.\overrightarrow{IB}+\overrightarrow{c}.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}\) (1)
Mặt khác:
\(\dfrac{ID}{IA}=\dfrac{BD}{AB}=\dfrac{CD}{AC}=\dfrac{BD+CD}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{a}{b+c}\)
\(\Leftrightarrow\left(b+c\right)\overrightarrow{ID}=-a.\overrightarrow{IA}\) (2)
(1); (2) \(\Rightarrow a.\overrightarrow{IA}+b.\overrightarrow{IB}+c.\overrightarrow{IC}=\left(b+c\right)\overrightarrow{ID}-\left(b+c\right)\overrightarrow{ID}=\overrightarrow{0}\)
Tổng bình phương các nghiệm của phương trình \(x^3+1=2\sqrt[3]{2x-1}\) trên tập số thực bằng
Đặt \(\sqrt[3]{2x-1}=t\Rightarrow2x=t^3+1\)
Ta được hệ: \(\left\{{}\begin{matrix}x^3+1=2t\\t^3+1=2x\end{matrix}\right.\)
\(\Rightarrow x^3-t^3=2t-2x\)
\(\Leftrightarrow\left(x-t\right)\left(x^2+xt+t^2\right)+2\left(x-t\right)=0\)
\(\Leftrightarrow\left(x-t\right)\left(x^2+xt+t^2+2\right)=0\)
\(\Leftrightarrow x=t\) (do \(x^2+xt+t^2+2=\left(x+\dfrac{t}{2}\right)^2+\dfrac{3t^2}{4}+2>0\))
\(\Leftrightarrow x=\sqrt[3]{2x-1}\Leftrightarrow x^3=2x-1\)
\(\Leftrightarrow x^3-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x-1\right)=0\)
Tới đây bấm máy hoặc dùng Viet
Tổng bình phương các nghiệm của phương trình \(x^3+1=2\sqrt[3]{x^2+5x-2}-2\) trên tập số thực bằng
Em kiểm tra lại đề bài, pt này chắc chắn là ko giải được
Tổng bình phương các nghiệm của phương trình 2 x + 1 + 3 − x = 1 + 3 + 2 x − x 2
A. 4
B. 8
C. 10
D. 9
Điều kiện: x + 1 ≥ 0 3 − x ≥ 0 x + 1 + 3 − x ≠ 0 ⇔ x ≥ − 1 x < 3 ⇔ − 1 ≤ x ≤ 3
Đặt: x + 1 + 3 − x = t t > 0
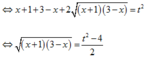
Khi đó, phương trình trở thành: 2 t = 1 + t 2 − 4 2 ⇔ 2 t = t 2 − 2 2
⇔ t 3 − 2 t − 4 = 0 ⇔ t − 2 t 2 + 2 t + 2 = 0 ⇔ t = 2
+ Với t = 2
⇔ x + 1 3 − x = 0 ⇔ x + 1 3 − x = 0 ⇔ x = − 1 ( t m ) x = 3 ( t m )
Tổng bình phương các nghiệm là: 10
Đáp án cần chọn là: C
Giải chi tiết hộ mk
1.Tổng bình phương các nghiệm nguyên của phương trình \(\left(2x+1\right)\left(x+1\right)^2\left(2x+3\right)=18\)
2.Tích các nghiệm của phương trình \(5\sqrt{x^3+1}=2\left(x^2+2\right)\)
Cảm ơn nhìu.
1/ nhân 4 cả 2 vế lên, vế trái sẽ trở thành (2x+1)(2x+2)^2(2x+3), nhân 2x+1 với 2x+3, cái bình phương phân tích ra
thành (4x^2+8x+3)(4x^2+8x+4)=72
đặt 4x^2+8x+4=a \(\left(a\ge0\right)\)
thay vào ta có (a-1)a=72 rồi bạn phân tích thành nhân tử sẽ có nghiệm là 9 và -8 loại được -8 thì nghiệm của a là 9
suy ra 2x+1=3 hoặc -3, tính ra được x rồi nhân vào với nhau
2/\(\Leftrightarrow5\sqrt{\left(x+1\right)\left(x^2-x+1\right)}=2\left[\left(x+1\right)+\left(x^2-x+1\right)\right]\)
đặt căn x+1=a, căn x^2-x+1=b (a,b>=0)
thay vào ra là \(2a^2-5ab+2b^2=0\\
\Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\)
suy ra a=2b hoặc b=2a, thay cái kia vào bình phương lên giải nốt phương trình rồi nhân nghiệm với nhau
Nghiệm nguyên.
2x+3=(2x+1)+2
\(\left(1\right)\Leftrightarrow\left[\left(2x+1\right)\left(x+1\right)\right]^2+2\left(2x+1\right)\left(x+1\right)^2=18\\ \)
2x+1 luôn lẻ---> x+1 phải chẵn --> x phải lẻ---> x=2n-1
\(\left(4n+3\right)\left(2n\right)^2\left(4n+1\right)=18\)
18 không chia hết co 4 vậy vô nghiệm nguyên.
Viết diễn dải dài suy luận logic rất nhanh
câu 2.
\(2\left(x^2+2\right)>0\forall x\) thực tế >=4 không cần vì mình cần so sánh với 0
\(\left(2\right)\Leftrightarrow25\left(x^3+1\right)=4\left(x^2+2\right)^2\)
Vậy đáp số là (16-25)/4=-9/4
tính tổng bình phương các nghiệm của phương trình: \(\sqrt{x-2}-3\sqrt{x^2-4}=0\)
ĐK: \(x\ge2\)
\(pt\Leftrightarrow\sqrt{x-2}=3\sqrt{x^2-4}\)
\(\Leftrightarrow x-2=9x^2-36\)
\(\Leftrightarrow9x^2-x-34=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{17}{9}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x^2=4\)