Tính đạo hàm cấp n của hàm số y = 2 x + 1 x + 2
A. 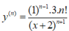
B. 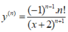
C. ![]()
D. ![]()
Trước hết ta xét: \(g\left(x\right)=\dfrac{1}{x+a}=\left(x+a\right)^{-1}\) với a là hằng số bất kì
\(g'\left(x\right)=-1.\left(x+a\right)^{-2}=\left(-1\right)^1.1!.\left(x+a\right)^{-\left(1+1\right)}\)
\(g''\left(x\right)=-1.\left(-2\right).\left(x+a\right)^{-3}=\left(-1\right)^2.2!.\left(x+a\right)^{-\left(2+1\right)}\)
Từ đó ta dễ dàng tổng quát được:
\(g^{\left(n\right)}\left(x\right)=\left(-1\right)^n.n!.\left(x+a\right)^{-\left(n+1\right)}=\dfrac{\left(-1\right)^n.n!}{\left(x+a\right)^{n+1}}\)
Xét: \(f\left(x\right)=\dfrac{x^2+1}{x\left(x-2\right)\left(x+2\right)}=-\dfrac{1}{4}.\left(\dfrac{1}{x}\right)+\dfrac{5}{8}\left(\dfrac{1}{x+2}\right)+\dfrac{5}{8}\left(\dfrac{1}{x-2}\right)\)
Áp dụng công thức trên ta được:
\(f^{\left(30\right)}\left(1\right)=\dfrac{1}{4}.\dfrac{\left(-1\right)^{30}.30!}{1^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1+2\right)^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1-2\right)^{31}}\)
Bạn tự rút gọn kết quả nhé
\(f\left(x\right)=\dfrac{x^2+1}{x^3}-4x\) hay \(f\left(x\right)=\dfrac{x^2+1}{x^3-4x}\) bạn?
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = {x^2} - x\);
b) \(y = \cos x\).
a: \(y'=\left(x^2-x\right)'=2x-1\)
\(y''=\left(2x-1\right)'=2\)
b: \(y'=\left(cosx\right)'=-sinx\)
\(y''=\left(-sinx\right)'=-cosx\)
Cho hàm số y = 1 x − 3 . Tính đạo hàm cấp hai của hàm số đã cho tại x = 1?
A. y " ( 1 ) = − 1 4
B. y " ( 1 ) = 1 4
C. y " ( 1 ) = 1 6
D. y " ( 1 ) = − 1 6
Đáp án A
Ta có: y ' = − 1 ( x − 3 ) 2 . ( x − 3 ) ' = − 1 ( x − 3 ) 2 y " = − 1 ( x − 3 ) 2 ' = − − 1 ( x − 3 ) 4 = 1 ( x − 3 ) 4 .2 ( x − 3 ) = 2 ( x − 3 ) 3 ;
⇒ y " ( 1 ) = 2 ( 1 − 3 ) 3 = − 1 4 .
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = 2{x^4} - 5{x^2} + 3\);
b) \(y = x{e^x}\).
\(a,y'=8x^3-10x\\ \Rightarrow y''=24x^2-10\\ b,y'=e^x+xe^x\\ \Rightarrow y''=e^x+e^x+xe^x=2e^x+xe^x\)
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = {x^3} - 4{x^2} + 2x - 3\);
b) \(y = {x^2}{e^x}\).
\(a,y'=3x^2-4x+2\\ \Rightarrow y''=6x-4\\ b,y'=2xe^x+x^2e^x\\ \Rightarrow y''=4xe^x+x^2e^x+2e^x\)
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = \ln \left( {x + 1} \right);\)
b) \(y = \tan 2x.\)
a: y=ln(x+1)
=>\(y'=\dfrac{1}{x+1}\)
=>\(y''=\dfrac{1'\left(x+1\right)-1\left(x+1\right)'}{\left(x+1\right)^2}=\dfrac{-1}{\left(x+1\right)^2}\)
b: y=tan 2x
=>\(y'=\dfrac{2}{cos^22x}\)
=>\(y''=\left(\dfrac{2}{cos^22x}\right)'=\dfrac{-2\cdot cos^22x'}{cos^42x}=\dfrac{-2\cdot2\cdot cos2x\left(cos2x\right)'}{cos^42x}\)
\(=\dfrac{4\cdot2\cdot sin2x}{cos^32x}=\dfrac{8\cdot sin2x}{cos^32x}\)
Tính đạo hàm cấp n của hàm số y = 2 x + 1
A. 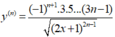
B. 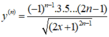
C. 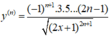
D. 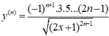
Tính đạo hàm cấp hai của các hàm số sau: y = 1 x 1 - x
Tính đạo hàm cấp hai của các hàm số sau: y = 1 1 - x
Tính đạo hàm cấp hai của các hàm số sau: y = 1 1 - x