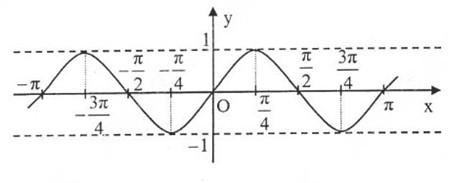
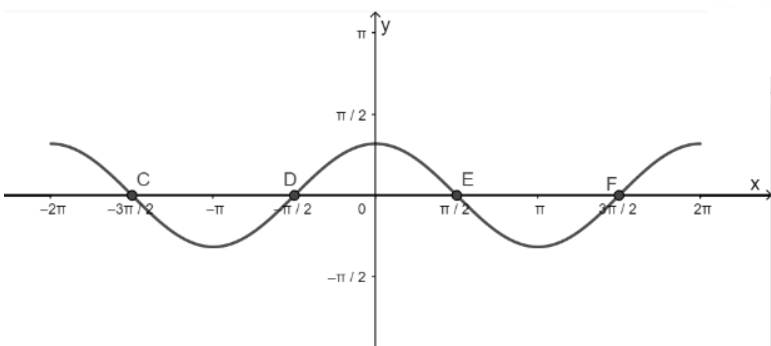
Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của x trên đoạn[-3π/2 ; 2π] để hàm số đó:
a. Nhận giá trị bằng – 1
b. Nhận giá trị âm
Căn cứ vào đồ thị hàm số \(y=\sin x\), tìm những giá trị của x trên đoạn \(\left[-\dfrac{3\pi}{2};2\pi\right]\) để hàm số đó :
a) Nhận giá trị bằng -1
b) Nhận giá trị âm
Đồ thị hàm số y = sin x trên đoạn [-2π, 2π]
Dựa vào đồ thị hàm số y = sinx
a) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị bằng -1 là:
x=−π2;x=3π2x=−π2;x=3π2
b) Những giá trị của x ∈ [−3π2,2π][−3π2,2π] để hàm số y = sin x nhận giá trị âm là:
x ∈ (-π, 0) ∪ (π, 2 π)
cho hàm số y = sinx, tìm những giá trị của x trên đoạn[-3π/2 ; 2π] để hàm số đó:
a. Nhận giá trị bằng 0
b. Nhận giá trị bằng -1/2
c. Nhận giá trị bằng giá trị dương
d. Nhận giá trị bằng giá trị âm
e. hàm số nhận giá trị \(\dfrac{\sqrt{3}}{2}\)
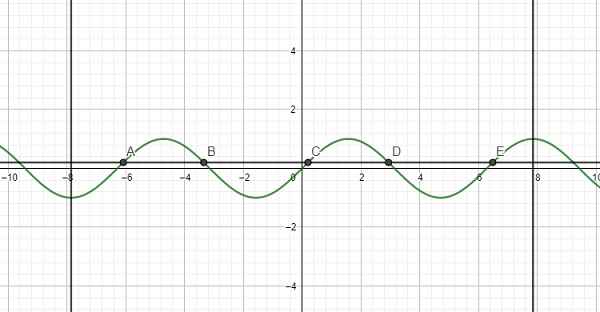
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) để:
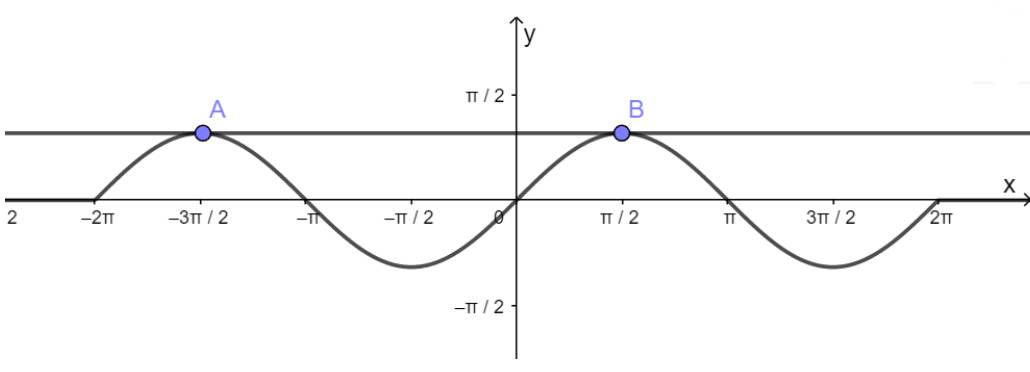
a) Hàm số y = sinx nhận giá trị bằng 1
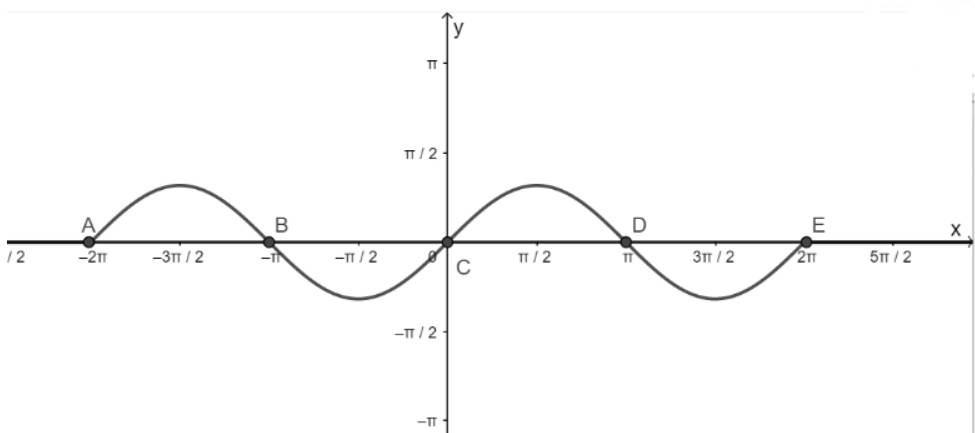
b) Hàm số y = sinx nhận giá trị bằng 0
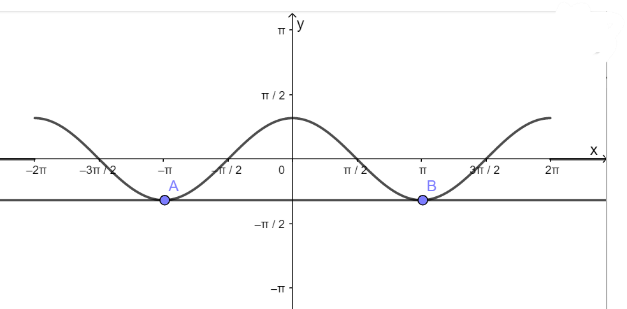
c) Hàm số y = cosx nhận giá trị bằng – 1
d) Hàm số y = cosx nhận giá trị bằng 0
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:

Vì

nên ta có đồ thị f(x) như sau:

Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,

Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
Dựa vào đồ thị của hàm số \(y = sinx\), xác định các giá trị \(x \in [ - \pi ;\pi ]\;\)thoả mãn \(sinx = \frac{1}{2}\)
Đồ thị của hàm số \(y=sin\left(x\right)\) trên đoạn \(\left[-\pi;\pi\right]\) là:

Ta thấy đồ thị hàm số giao với đường thẳng d: \(y=\dfrac{1}{2}\) tại 2 điểm.
Do đó, phương trình \(sin\left(x\right)=\dfrac{1}{2}\) có hai giá trị \(x\in\left[-\pi;\pi\right]\) thỏa mãn
Dựa vào đồ thị của hàm số y=sinx hãy tìm số nghiệm của phương trình: sinx=1/2018 trên đoạn \(\left[-\dfrac{5\pi}{2};\dfrac{5\pi}{2}\right]\)
\(0< \dfrac{1}{2018}< 1\)
Kẻ 1 đường thẳng nằm ngang nằm giữa \(y=0\) và \(y=1\) ta thấy cắt đồ thị tại 5 điểm trên đoạn đã cho
\(\Rightarrow\) Pt có 5 nghiệm
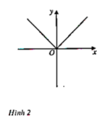
Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [(-π)/2; 3π/2] và các hàm số y = |x| trên khoảng (-∞; +∞)
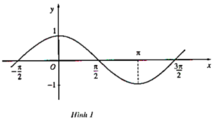
- Hàm số y = cosx trên đoạn [(-π)/2; 3π/2]:
Các khoảng tăng: [(-π)/2,0], [π, 3π/2].
Các khoảng giảm: [0, π ],.
- Hàm số y = |x| trên khoảng (-∞; +∞)
Khoảng tăng: [0, +∞)
Khoảng giảm (-∞, 0].
ừ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [(-π)/2; 3π/2] và các hàm số y = |x| trên khoảng (-∞; +∞).
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=sinx+cosx+mx đồng biến trên khoảng - ∞ ; + ∞
A . - 2 ≤ m ≤ 2
B . m ≤ - 2
C . - 2 < m < 2
D . m ≥ 2