- Hàm số y = cosx trên đoạn [(-π)/2; 3π/2]:
Các khoảng tăng: [(-π)/2,0], [π, 3π/2].
Các khoảng giảm: [0, π ],.
- Hàm số y = |x| trên khoảng (-∞; +∞)
Khoảng tăng: [0, +∞)
Khoảng giảm (-∞, 0].
- Hàm số y = cosx trên đoạn [(-π)/2; 3π/2]:
Các khoảng tăng: [(-π)/2,0], [π, 3π/2].
Các khoảng giảm: [0, π ],.
- Hàm số y = |x| trên khoảng (-∞; +∞)
Khoảng tăng: [0, +∞)
Khoảng giảm (-∞, 0].
Từ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [(-π)/2; 3π/2] và các hàm số y = |x| trên khoảng (-∞; +∞).
ừ đồ thị (H.1, H.2) hãy chỉ ra các khoảng tăng, giảm của hàm số y = cosx trên đoạn [(-π)/2; 3π/2] và các hàm số y = |x| trên khoảng (-∞; +∞).
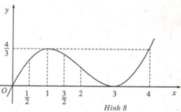
Dựa vào đồ thị (H.7, H.8), hãy chỉ ra các điểm tại đó mỗi hàm số sau có giá trị lớn nhất (nhỏ nhất):
y = x/3(x+ 3)2 trong các khoảng (1/2; 3/2) và (3/2; 4)
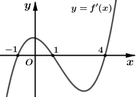
Cho hàm số y=f(x) liên tục trên đoạn [1;4] và có đồ thị hàm số y=f'(x) như hình bên. Hỏi hàm số g(x)=f( x 2 + 2 ) nghịch biến trên khoảng nào trong các khoảng sau?
![]()
![]()
![]()
![]()
Cho hàm số y= f(x) có đạo hàm trên R thoả f( 2) = f( -2) =0 và đồ thị của hàm số y= f’ (x) có dạng như hình bên. Hàm số y= (f( x)) 2 nghịch biến trên khoảng nào trong các khoảng sau ?
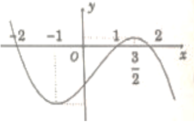
A. - 1 ; 3 2
B. (-1; 1)
C. (-2; -1)
D. (1; 2)
Cho hàm số y=f(x) liên tục trên đoạn [-1;4] và có đồ thị hàm số y=f’(x) như hình bên. Hỏi hàm số g ( x ) = f x 2 + 1 nghịch biến trên khoảng nào trong các khoảng sau?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y= f(x). Đồ thị hàm số y= f’(x) như hình dưới và f(-2) = f( 2) = 0
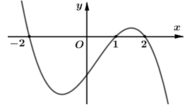
Hàm số g( x) = [ f( 3-x)]2 nghịch biến trên khoảng nào trong các khoảng sau?
A. (- 2; -1)
B. (1; 2)
C. (2; 5)
D. ( 5 ; + ∞ )
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Đồ thị hàm số y= f’(x) như hình bên.
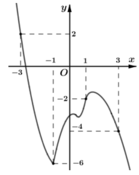
Hỏi hàm số g(x) = 2f(x) + (x+ 1)2 đồng biến trên khoảng nào trong các khoảng sau?
A. (-3; 1)
B. (1; 3)
C. ( - ∞ ; 3 )
D. (3; + ∞ )
Cho hàm số y = f(x) có đạo hàm liên tục trên i. Đồ thị hàm số y = f’(x) như hình bên dưới
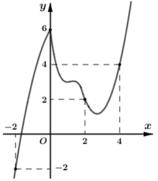
Hàm số g(x) = 2 f(x) - x 2 đồng biến trên khoảng nào trong các khoảng sau đây?
![]()
![]()
![]()
![]()