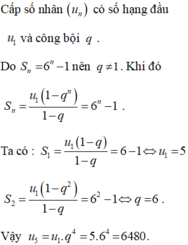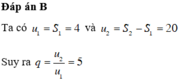Tìm số các số hạng của cấp số nhân ( u n ) biết u 1 = 2 , u n = 1 8 , S n = 31 8
PB
Những câu hỏi liên quan
Cho cấp số cộng (un) có số hạng đầu là u = 1 và công sai d = 1. Tìm n sao cho tổng n số hạng đầu tiên của cấp số cộng đó bằng 3003
Xem chi tiết
Theo đề, ta có: \(S_n=3003\)
=>\(n\cdot\dfrac{\left[2u1+\left(n-1\right)\cdot d\right]}{2}=3003\)
=>\(\dfrac{n\left[2+\left(n-1\right)\right]}{2}=3003\)
=>n(n+1)=6006
=>n^2+n-6006=0
=>(n-77)(n+78)=0
=>n=77(nhận) hoặc n=-78(loại)
Vậy: n=77
Đúng 2
Bình luận (0)
Bài 1: Cho cấp số nhân có: u3 = 18 và u6 = -486.
Tìm số hạng đầu tiên và công bội q của cấp số nhân đó
Bài 2: Tìm u và q của cấp số nhân (un) biết:
Bài 3: Tìm cấp số nhân (un) biết cấp số đó có 4 số hạng có tổng bằng 360 và số hạng cuối gấp 9 lần số hạng thứ hai.
Một cấp số cộng và một cấp số nhân có số hạng thứ nhất bằng 5, số hạng thứ hai của cấp số cộng lớn hơn số hạng thứ hai của cấp số nhân là 10, còn các số hạng thứ ba bằng nhau. Tìm các cấp số ấy.
ĐS: Cấp số cộng: 5, 25, 45
Cấp số nhân: 5, 15, 45
Đúng 0
Bình luận (0)
Một cấp số nhân dương có 4 số hạng, công bội q bằng 1/4 lần số hạng thứ nhất, tổng của hai số hạng đầu bằng 24. Tìm tích các số hạng cấp số nhân đó?
A. 2
B. 1
C. 4096
D. 262144
Một cấp số cộng và một cấp số nhân có số hạng thứ nhất bằng 5, số hạng thứ hai của cấp số cộng lớn hơn số hạng thứ hai của cấp số nhân là 10, còn các số hạng thứ 3 bằng nhau. Tìm các cấp số ấy ?
Gọi 3 số hạng của cấp số cộng là: \(5;5+d;5+2d\)
Gọi 3 số hạng của cấp số nhân là: \(5;5q;5q^2\).
Ta có hệ sau:\(\left\{{}\begin{matrix}5+2d=5q^2\\5+d=5q+10\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}5+2d=5q^2\\d=5q+5\end{matrix}\right.\)\(\Rightarrow5+2.\left(5q+5\right)=5q^2\)\(\Rightarrow\left\{{}\begin{matrix}q=-1\\q=3\end{matrix}\right.\).
Với \(q=-1\) thì \(d=5.q+5=5.\left(-1\right)+5=0\).
Với \(q=3\) thì \(d=5.q+5=5.3+5=20\).
Vậy
Với \(q=-1\):
3 số hạng của cấp số cộng là: 5; 5; 5.
3 số hạng của cấp số nhân là: 5; - 5; 5.
Với \(q=3\):
3 số hạng của cấp số cộng là: 5; 25; 45.
3 số hạng của cấp số nhân là: 5; 15; 45.
Đúng 0
Bình luận (0)
Tìm các số hạng của cấp số nhân u n có năm số hạng, biết: u 3 = 3 và u 5 = 27
Ta có: u3 = u1.q2 ; u5 = u1.q5.
Theo đề bài, ta có hệ phương trình :
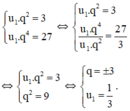
+ Với q = 3 ta có cấp số nhân : 1/3 ; 1 ; 3 ; 9 ; 27.
+ Với q = -3 ta có cấp số nhân : 1/3 ; -1 ; 3 ; -9 ; 27.
Đúng 0
Bình luận (0)
Cho cấp số nhân
u
n
có tổng
n
số hạng đầu tiên là
S
n
6
n
-
1
. Tìm số hạng thứ năm của cấp số nhân đã cho A. 120005 B. 6840 C. 7775 D. 6480
Đọc tiếp
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số nhân đã cho
A. 120005
B. 6840
C. 7775
D. 6480
Chọn D
Cấp số nhân u n có số hạng đầu u 1 và công bội q
Do S n = 6 n - 1 nên q ≠ 1
Khi đó S n = u 1 ( 1 - q n ) 1 - q = 6 n - 1
Ta có : S 1 = u 1 ( 1 - q ) 1 - q ⇔ u 1 = 5
S 2 = u 1 1 - q 2 1 - q ⇔ q = 6
Vậy u 5 = u 1 . q 4 = 6480
Đúng 0
Bình luận (0)
Cho cấp số nhân
u
n
có tổng n số hạng đầu tiên là
S
n
6
n
-
1
. Tìm số hạng thứ năm của cấp số nhân đã cho. A. 120005 B. 6840 C. 7775 D. 6480
Đọc tiếp
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 6 n - 1 . Tìm số hạng thứ năm của cấp số nhân đã cho.
A. 120005
B. 6840
C. 7775
D. 6480
Cho cấp số nhân
u
n
có tổng n số hạng đầu tiên là
S
n
5
n
−
1
,
n
1
,
2
,
3
...
Tìm số hạng đầu
u
1
và công bội q của cấp số nhân đó. A.
u
1
5...
Đọc tiếp
Cho cấp số nhân u n có tổng n số hạng đầu tiên là S n = 5 n − 1 , n = 1 , 2 , 3 ... Tìm số hạng đầu u 1 và công bội q của cấp số nhân đó.
A. u 1 = 5 , q = 6
B. u 1 = 4 , q = 5
C. u 1 = 5 , q = 4
D. u 1 = 6 , q = 5
Ai đó làm ơn giúp mình với ạ, mình cảm ơn rất nhiều 1.Cho cấp số nhân(Un). Tìm U1 và q. Biết rằng a. U1 + u6= 165; u3 + u4=60 2. Tìm số hạng đầu và công bội của cấp số nhân, biết a. U4- u2= 72; U5- u3=144 b. u1- u3+u5=65;u1+u7=325 c. u3+u5=90; u2-u6=240 d. u1+u2+u3=14; u1.u2.u3=64
Để tìm U1 và q, ta sử dụng hệ phương trình sau:
U1 + U6 = 165U3 + U4 = 60Đầu tiên, ta sử dụng phương trình thứ hai để tìm U3: U3 = 60 - U4
Sau đó, thay giá trị của U3 vào phương trình thứ nhất: U1 + U6 = 165 U1 + (U3 + 3q) = 165 U1 + (60 - U4 + 3q) = 165 U1 - U4 + 3q = 105 (1)
Tiếp theo, ta sử dụng phương trình thứ nhất để tìm U6: U6 = 165 - U1
Thay giá trị của U6 vào phương trình thứ hai: U3 + U4 = 60 (60 - U4) + U4 = 60 60 = 60 (2)
Từ phương trình (2), ta thấy rằng phương trình không chứa U4, do đó không thể giải ra giá trị của U4. Vì vậy, không thể tìm được giá trị cụ thể của U1 và q chỉ từ hai phương trình đã cho.
Để tìm số hạng đầu và công bội của cấp số nhân, ta sử dụng các phương trình đã cho:
a. U4 - U2 = 72 U5 - U3 = 144
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U4: U4 = U2 + 72
Sau đó, thay giá trị của U4 vào phương trình thứ hai: U5 - U3 = 144 (U2 + 2q) - U3 = 144 U2 - U3 + 2q = 144 (3)
Từ phương trình (3), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
b. U1 - U3 + U5 = 65 U1 + U7 = 325
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U7: U7 = 325 - U1
Sau đó, thay giá trị của U7 vào phương trình thứ nhất: U1 - U3 + U5 = 65 U1 - U3 + (U1 + 6q) = 65 2U1 - U3 + 6q = 65 (4)
Từ phương trình (4), ta thấy rằng phương trình không chứa U3, do đó không thể giải ra giá trị của U1 và q chỉ từ hai phương trình đã cho.
c. U3 + U5 = 90 U2 - U6 = 240
Đầu tiên, ta sử dụng phương trình thứ hai để tìm U6: U6 = U2 - 240
Sau đó, thay giá trị của U6 vào phương trình thứ nhất: U3 + U5 = 90 U3 + (U2 - 240 + 4q) = 90 U3 + U2 - 240 + 4q = 90 U3 + U2 + 4q = 330 (5)
Từ phương trình (5), ta thấy rằng phương trình không chứa U2, do đó không thể giải ra giá trị của U2 và q chỉ từ hai phương trình đã cho.
d. U1 + U2 + U3 = 14 U1 * U2 * U3 = 64
Đầu tiên, ta sử dụng phương trình thứ nhất để tìm U3: U3 = 14 - U1 - U2
Sau đó, thay giá trị của U3 vào phương trình thứ hai: U1 * U2 * (14 - U1 - U2) = 64
Phương trình này có dạng bậc ba và không thể giải ra giá trị cụ thể của U1 và U2 chỉ từ hai phương trình đã cho.
Tóm lại, không thể tìm được giá trị cụ thể của số hạng đầu và công bội của cấp số nhân chỉ từ các phương trình đã cho.
Đúng 0
Bình luận (0)