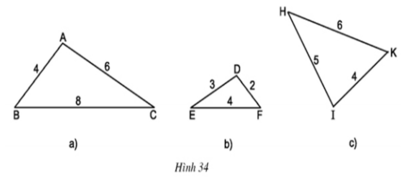
Tìm trong hình 34 các cặp tam giác đồng dạng:
Tìm trong Hình 4 các cặp tam giác đồng dạng.
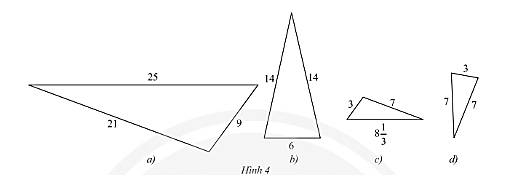
Xét cặp tam giác thứ nhất: Hình a và Hình c.
Ta có: \(\frac{3}{9} = \frac{1}{3};\frac{7}{{21}} = \frac{1}{3};\frac{{8\frac{1}{3}}}{{25}} = \frac{1}{3}\).
Do đó, tam giác ở Hình a và Hình c đồng dạng với nhau.
Xét cặp tam giác thứ hai: Hình b và Hình d.
Ta có: \(\frac{7}{{14}} = \frac{1}{2};\frac{7}{{14}} = \frac{1}{2};\frac{3}{6} = \frac{1}{2}\).
Do đó, tam giác ở Hình b và Hình d đồng dạng với nhau.
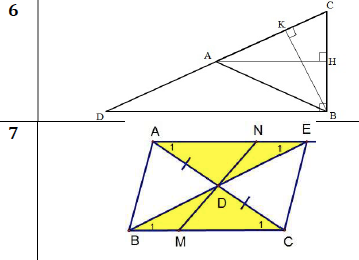
giúp mình tìm các cặp tam giác đồng dạng trong 2 hình này với
Câu 6:
\(\left\{{}\begin{matrix}\widehat{ACB}\text{ chung}\\\widehat{CKB}=\widehat{CHA}=90^0\end{matrix}\right.\Rightarrow\Delta CHA\sim\Delta CKB\left(g.g\right)\\ \left\{{}\begin{matrix}\widehat{ACB}\text{ chung}\\\widehat{AHC}=\widehat{DBC}=90^0\end{matrix}\right.\Rightarrow\Delta CHA\sim\Delta CBD\left(g.g\right)\\ \left\{{}\begin{matrix}\widehat{ACB}\text{ chung}\\\widehat{CKB}=\widehat{DBA}=90^0\end{matrix}\right.\Rightarrow\Delta CKB\sim\Delta CBD\left(g.g\right)\\ \Delta CHA\sim\Delta CKB\Rightarrow\dfrac{CH}{CK}=\dfrac{CA}{CB}\Rightarrow\Delta CKH\sim\Delta CBA\left(c.g.c\right)\)
6 ADB và ACB
7 AE và BC , AB và EC
Cho hình bên là tam giác ABC vuông tại A, đường cao AH. Trong hình bên có bao nhiêu cặp tam giác đồng dạng với nhau. Hãy chỉ ra các cặp đồng dạng và theo các đỉnh tương ứng.
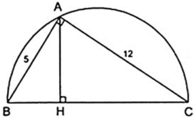
Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.
Hãy chỉ ra các cặp tam giác đồng dạng trong hình 47.
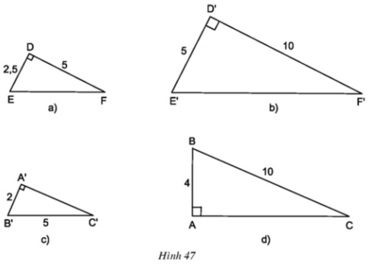
+ΔDEF vuông tại D và ΔD'E'F' vuông tại D’ có:
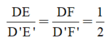
⇒ ΔDEF ∼ ΔD'E'F' (hai cạnh góc vuông)
*)Áp dụng định lí py ta go vào tam giác A’B’C’ vuông tại A’ có:
A’C’2 + A’B’2 = B’C’2
=> A’C’2 + 22 = 52
Suy ra: A’C’2 = 25 – 4 = 21 nên 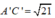
*)Áp dụng định lí py ta go vào tam giác ABC vuông tại A có:
AB2 + AC2 = BC2
Thay số: 42 + AC2 = 102
Suy ra: AC2 = 100 – 16 = 84 nên

Do đó, ∆ A’B’C’ đồng dạng với tam giác ABC ( trường hợp 2).
Hãy chỉ ra các cặp tam giác vuông đồng dạng với nhau trong Hình 9.52, viết đúng kí hiệu đồng dạng.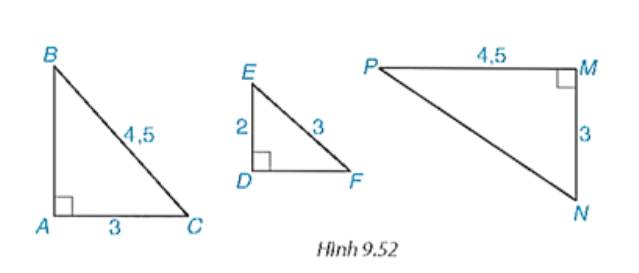
Ta có:
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)
Cho tam giác vuông ABC (góc A= 90 độ), đường cao AH. Tìm tất cả các cặp tam giác đồng dạng với nhau có trong hình và giải thích tại sao?
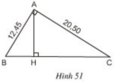
Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).
b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.
a) ΔABC 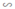 ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC 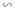 ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA 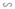 ΔHAC vì cùng đồng dạng với ΔABC.
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)

cho hình bình hành ABCD có độ dài các cạnh AB =12cm BC =7cm trên cạnh AB lấy điểm E sao cho AE =8cm đường thẳng DE cắt cạnh CB kéo dài tại F
a) trong hình vẽ có tất cả bao nhiêu cặp tam giác đồng dạng vs nhau hãy viết tên các cặp tam giác đồng dạng vs nhau theo các đỉnh tương ứng
a: Xét ΔFEB và ΔFDC có
góc FEB=góc FDC
góc F chung
=>ΔFEB đồng dạng với ΔFDC
Xét ΔEAD và ΔEBF có
góc EAD=góc EBF
góc AED=góc FEB
=>ΔEAD đồng dạng với ΔEBF
Xét ΔABD và ΔCDB có
góc ABD=góc CDB
góc A=góc C
=>ΔABD đồng dạng với ΔCDB
Xét ΔABC và ΔCDA có
góc ABC=góc CDA
góc BAC=góc DCA
=>ΔABC đồng dạng với ΔCDA
Trên hình vẽ hãy chỉ ra các tam giác đồng dạng .Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng
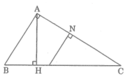
- △ ABC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ở đỉnh B chung
- △ ABC đồng dạng △ HAC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ ABC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ∠ (HBA) = ∠ (HAC)
- △ HAB đồng dạng △ NCM
Hai tam giác vuông có góc nhọn ∠ (HAB) = ∠ (NCM)