Tính số đo mỗi góc nhọn của một tam giác vuông cân
PB
Những câu hỏi liên quan
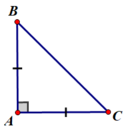
a) tính số đo mỗi góc nhọn của tam giác ABC vuông cân tại A
b) cho tam giác ABC . Biết AB=11cm;AC=15cm; BC=19cm
so sánh các góc của tam giác ABC
a, Do ABC vuông cân
=> Góc A = 90 độ
=> Góc B = Góc C = 90/2 = 45 độ
b, Do AB < AC < BC (11 < 15 < 19)
=> Góc C < Góc B < Góc A (Quan hệ góc đối diện)
Đúng 1
Bình luận (0)
Cho tam giác ABC đều . Vẽ bên ngoài tam giác này 2 tam giác vuông cân . tam giác ABD vuông cân tại B, tam giác ACE vuông cân tại C. Tính số đo góc nhọn tam giác ADE
Ta có: ΔABD vuông cân tại B(gt)
nên \(\widehat{DAB}=45^0\)(Số đo của một góc nhọn trong ΔABD vuông cân tại B)
Ta có: ΔACE vuông cân tại C(gt)
nên \(\widehat{EAC}=45^0\)(Số đo của một góc nhọn trong ΔACE vuông cân tại C)
Ta có: ΔABC đều(gt)
nên AB=AC=BC và \(\widehat{BAC}=60^0\)(Số đo của các cạnh và các góc trong ΔABC đều)(1)
Ta có: \(\widehat{DAE}=\widehat{DAB}+\widehat{BAC}+\widehat{EAC}\)
\(\Leftrightarrow\widehat{DAE}=60^0+45^0+45^0=150^0\)
Ta có: ΔADB vuông cân tại B(gt)
nên AB=BD(hai cạnh bên)(2)
Ta có: ΔACE vuông cân tại C(gt)
nên AC=CE(hai cạnh bên)(3)
Từ (1), (2) và (3) suy ra AB=BC=AC=CE=DB
Xét ΔABD vuông tại B và ΔACE vuông tại C có
AB=AC(cmt)
DB=EC(cmt)
Do đó: ΔABD=ΔACE(hai cạnh góc vuông)
hay AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
hay \(\widehat{ADE}=\widehat{AED}=\dfrac{180^0-\widehat{DAE}}{2}\)(Số đo của các góc ở đáy trong ΔADE cân tại A)
hay \(\widehat{ADE}=15^0\) và \(\widehat{AED}=15^0\)
Vậy: Số đo các góc nhọn trong ΔADE là 150
Đúng 3
Bình luận (1)
Cho tam giác ABC đều . Vẽ bên ngoài tam giác này 2 tam giác vuông cân . tam giác ABD vuông cân tại B, tam giác ACE vuông cân tại C. Tính số đo góc nhọn tam giác ADE
vẽ hình giati chi tiết mình tick nhá
VM
7 tháng 1 2022 lúc 20:34
Cho biết tỉ số hai góc nhọn trong một tam giác vuông là 0,8 , tìm số đo mỗi góc nhọn ấy.
số đo hai góc lần lượt là 400 và 500
Đúng 1
Bình luận (1)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{a+b}{4+5}=\dfrac{90}{9}=10\)
Do đó: a=40; b=50
Đúng 1
Bình luận (0)
a) Góc ngoài của một tam giác cân có số đo bằng 1300 . Tính số đo các góc tam giác đó. b) Góc ngoài của một tam giác cân có số đo bằng 800 . Tính số đo các góc tam giác đó.
- Nêu các trường hợp bằng nhau của hai tam giác.- Nêu các trường hợp bằng nhau của hai tam giác vuông.- Thế nào là tam giác cân? Nêu các tính chất của tam giác cân? Nêu các cách để chứng minh tam giác cân- Thế nào là tam giác vuông cân? Nêu các tính chất của tam giác vuông cân? Số đo mỗi góc nhọn trong tam giác vuông cân là bao nhiêu?Thế nào là tam giác đều? Nêu các tính chất
Đọc tiếp
- Nêu các trường hợp bằng nhau của hai tam giác.
- Nêu các trường hợp bằng nhau của hai tam giác vuông.
- Thế nào là tam giác cân? Nêu các tính chất của tam giác cân? Nêu các cách để chứng minh tam giác cân
- Thế nào là tam giác vuông cân? Nêu các tính chất của tam giác vuông cân? Số đo mỗi góc nhọn trong tam giác vuông cân là bao nhiêu?
Thế nào là tam giác đều? Nêu các tính chất
Cho tam giác ABC vuông có hai góc nhọn B và C hơn kém nhau 24 độ .Tính số đo của mỗi góc
- Phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh • các dụngm giác là tam giác cân.(5) Phát biểu định nghĩa và tính chất tam giác đều. Nêu các cách chứng minh tam giác là tam giác đều.(6) Phát biểu định lí Py-ta-go thuận và đảo. b) Trả lời các câu hỏi sau(1) Thế nào là hai tam giác bằng nhau? đến đo (2) Thế nào là tam giác cân?(3) Thế nào là tam giác vuông cân? (4) Thế nào là tam giác đều? (5) Nêu các tính chất của tam giác cân. (6) Nêu các tính chất của tam giác vuông câ...
Đọc tiếp
- Phát biểu định nghĩa và tính chất tam giác cân. Nêu các cách chứng minh • các dụng
m giác là tam giác cân.
(5) Phát biểu định nghĩa và tính chất tam giác đều. Nêu các cách chứng minh tam giác là tam giác đều.
(6) Phát biểu định lí Py-ta-go thuận và đảo. b) Trả lời các câu hỏi sau
(1) Thế nào là hai tam giác bằng nhau? đến đo (2) Thế nào là tam giác cân?
(3) Thế nào là tam giác vuông cân? (4) Thế nào là tam giác đều? (5) Nêu các tính chất của tam giác cân. (6) Nêu các tính chất của tam giác vuông cân. (7) Nêu các tính chất của tam giác đều. c) Đố bạn nêu chính xác các tính chất sau: (1) Nếu ba cạnh của tam giác này .... tam giác kia, thì hai tam giác đó bằng
(2) Nếu hai cạnh và góc xen giữa của tam giác này .... tam giác kia, thì giác đó bằng nhau.
(3) Nếu một cạnh và hai góc kề của tam giác này .... tam giác kia, thì hai ta đó bằng nhau.
(4) Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vụ .... tam giác vuông kia, thì hai tam giác đó bằng nhau.
(5) Nếu cạnh huyền và một góc nhọn của tam giác vuông này .... tam giá kia, thì hai tam giác đó bằng nhau. | (6) Nếu hai cạnh góc vuông của tam giác vuông này .... tam giác vuông ki tam giác đó bằng nhau.
6 tính chất tam giác vuông cân
(7) Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này .... vuông kia, thì hai tam giác đó bằng nhau.
(8) Trong một tam giác vuông, bình phương của cạnh huyền bằng... cạnh g (9) Nếu một tam giác có bình phương của một cạnh bằng... đó là tam gi
Please! Gấp! T^T
1 Cho tam giác ABC cân tại A và tam giác đều BCD (D và A nằm phía đối với BC). Tính số đo góc BDA.
2 Chứng minh rằng góc ở đáy của một tam giác cân bao giờ cũng là góc nhọn.