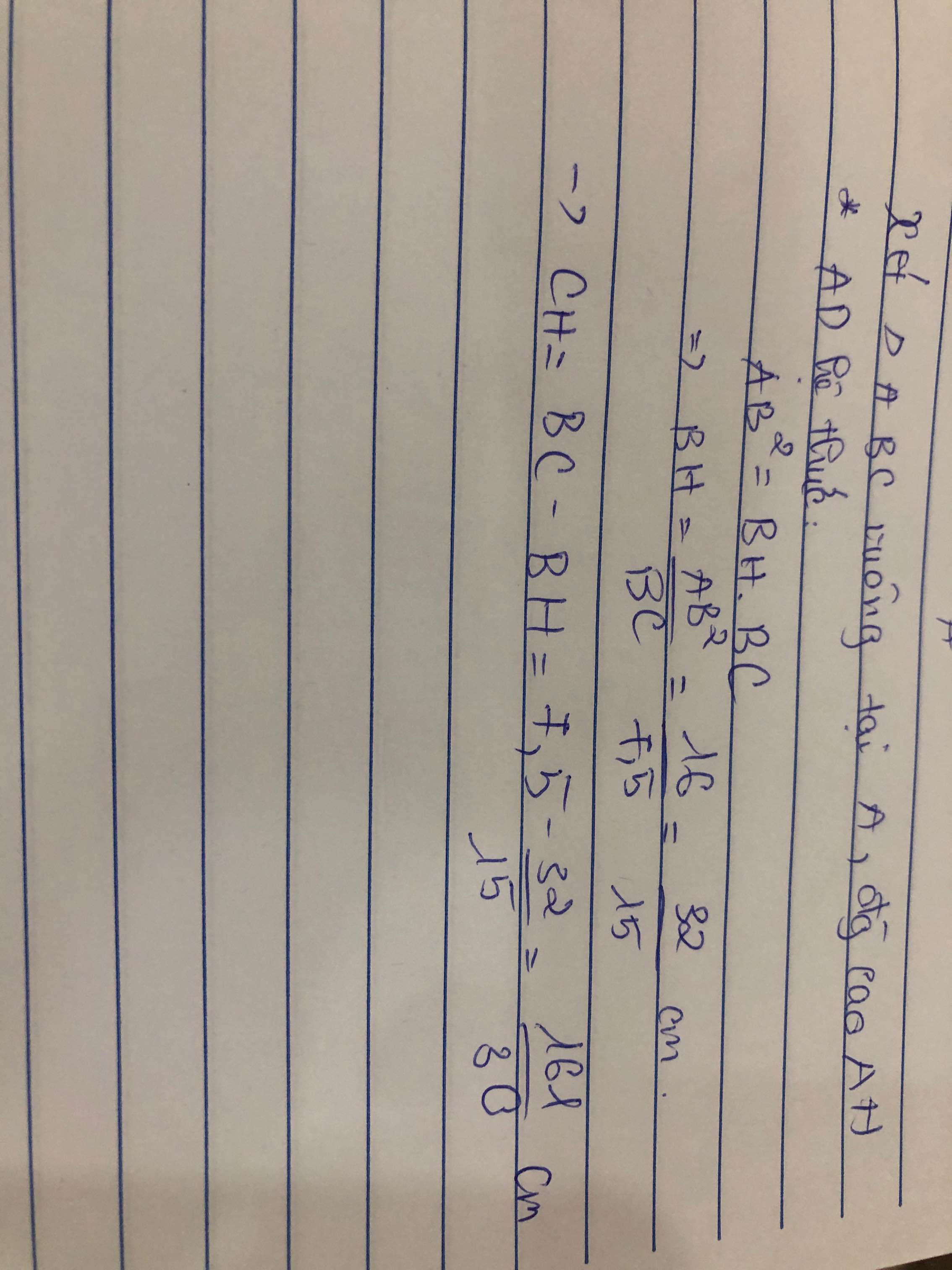Cho tam giác ABC vuông tại A. AB = 7,5 cm; BC = 12,5cm.
a) Tính diện tích tam giác ABC.
b) Lấy điểm M trên cạnh AB sao cho AM: MB = 1:2. Từ M kẻ đường thẳng song song với BC cắt trung tuyến AF tại E và cắt cạnh AC tại N. Chứng minh E là trung điểm của MN.
c) Gọi G, H, I thứ tự là trung điểm của MC, NB và FE. Chứng minh G, H, I thẳng hàng và tính diện tích ∆IHF