Cho hai hàm số y = − 1 2 x 2 và y = x − 4 có đồ thị lần lượt là ( P ) và ( d )
1) Vẽ hai đồ thị ( P ) và ( d ) trên cùng một mặt phẳng tọa độ.
2 ) Tìm tọa độ giao điểm của hai đồ thị ( P ) và ( d ).
Chọn câu trl sai Cho hai hàm số y= (a+ 1 )x - 2 và y= -x +1 A. Hàm số y= (a+1)x-2 đồng biến khi a
Hàm số y=(a+1)x-2 đồng biến khi a+1>0
=>a>-1
a) Vẽ đồ thị của hàm số sau y = 2x + 2 b) Cho hai hàm số y = (2k + 2) * x - 3 và y = (1 - 3k) * x + 2 Với giá trị nào của k thi đồ thị của hai hàm số là hai đường thẳng cắt nhau ?
b: Để hai đường cắt nhau thì 2k+2<>1-3k
=>5k<>-1
=>k<>-1/5
Bài 1: Cho hai hàm số bậc nhất: y= (k+1)x + 3 ; y= (3-2k)x + 1 a)Vẽ đồ thị của hai hàm số trên khi k=2 - Khi k=2 thì ta có hai hàm số : y= 3x+3 và y= -x+1 b) Tìm tọa độ giao điểm của đồ thị hàm số vừa vẽ. c) Tìm góc tạo bởi đường thẳng y= 3x+3 vớt trục Ox ( làm tròn đến phút ) giải giúp mik vs ak!! mik đang cần gấp lắm!!
a)
Thay x=0 vào hàm số y= 3x+3, ta được: y= 3 x 0 + 3 = 3
Thay y=0 vào hàm số y= 3x+3, ta được: 0= 3x+3 => x= -1
Vậy đồ thị hàm số đi qua điểm B(-1;0) và C(0;3)
Thay x=0 vào hàm số y= -x+1, ta được: y= -0 + 1 = 1
Thay y=0 vào hàm số y= -x+1, ta được: 0= -x+1 => x= 1
(Có gì bạn tự vẽ đồ thị nha :<< mình không load hình được sorry bạn nhiều)
b) Hoành độ giao điểm của hai đường thằng y=3x+3 và y=-x+1 :
3x+3 = -x+1
<=> 3x + x = 1 - 3
<=> 4x = -2
<=> x= - \(\dfrac{1}{2}\)
Thay x= - \(\dfrac{1}{2}\) vào hàm số y= -x+1, ta được: y= \(\dfrac{1}{2}\)+1 = \(\dfrac{3}{2}\)
Vậy giao điểm của hai đường thằng có tọa độ (\(-\dfrac{1}{2};\dfrac{3}{2}\))
c) Gọi góc tạo bởi đường thẳng y= 3x+3 là α
OB= \(\left|x_B\right|=\left|-1\right|=1\)
OC= \(\left|y_C\right|=\left|3\right|=3\)
Xét △OBC (O= 90*), có:
\(tan_{\alpha}=\dfrac{OC}{OB}=\dfrac{3}{1}=3\)
=> α= 71*34'
Vậy góc tạo bởi đường thằng y=3x+3 là 71*34'
Cho hai hàm số f(x)=x+2 và g ( x ) = x 2 - 2 x + 3 Đạo hàm của hàm số y = g f x tại x=1 bằng
A. 4
B. 1
C. 3
D. 2
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: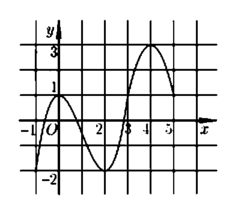
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Đáp án D
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.
Bài 1 : Cho hai hàm số bậc nhất y = 3mx + 2 và y = (2m + 1)x + 3. Tìm giá trị của m để
đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng cắt nhau
b) Hai đường thẳng song song.
Bài 2 : Cho hai hàm số bậc nhất (d1): y = 3mx + 4 – m2
và (d2): y = (2m + 1)x + 3. Tìm
giá trị của m để đồ thị của hai hàm số đó:
a) Cắt nhau. b) Trùng nhau
b) Song song với nhau d) Vuông góc với nhau.
Bài 1
ĐKXĐ: m ≠ 0 và m ≠ -1/2
a) Để hai đường thẳng cắt nhau thì:
3m ≠ 2m + 1
⇔ m ≠ 1
Vậy m ≠ 0; m ≠ -1/2 và m ≠ 1 thì hai đường thẳng đã cho cắt nhau
b) Để hai đường thẳng song song thì:
3m = 2m + 1
⇔ m = 1 (nhận)
Vậy m = 1 thì hai đường thẳng đã cho song song
Bài 2
ĐKXĐ: m ≠ 0 và m ≠ -1/2
a) Để hai đường thẳng đã cho cắt nhau thì:
3m ≠ 2m + 1
⇔ m ≠ 1
Vậy m ≠ 0; m ≠ -1/2; m ≠ 1 thì hai đường thẳng đã cho cắt nhau
b) Để hai đường thẳng trùng nhau thì:
3m = 2m + 1 và 4 - m² = 3
*) 3m = 2m + 1
⇔ m = 1 (nhận) (*)
*) 4 - m² = 3
⇔ m² = 4 - 3
⇔ m² = 1
⇔ m = 1 (nhận) hoặc m = -1 (nhận) (**)
Từ (*) và (**) ⇒ m = 1 thì hai đường thẳng đã cho trùng nhau
c) Để hai đường thẳng đã cho song song thì:
3m = 2m + 1 và 4 - m² ≠ 3
*) 3m = 2m + 1
⇔ m = 1 (nhận) (1)
*) 4 - m² ≠ 3
⇔ m² ≠ 1
⇔ m ≠ 1 (nhận) và m ≠ -1 (nhận) (2)
Từ (1) và (2) ⇒ Không tìm được m để hai đường thẳng đã cho song song
d) Để hai đường thẳng vuông góc thì:
3m.(2m + 1) = -1
⇔ 6m² + 3m + 1 = 0 (3)
Ta có:
6m² + 3m + 1 = 6.(m² + m/2 + 1/6)
= 6.(m² + 2.m.1/4 + 1/16 + 5/48)
= 6(m + 1/4)² + 5/8 > 0 (với mọi m)
⇒ (3) là vô lý
Vậy không tìm được m để hai đường thẳng đã cho vuông góc
Cho hai hàm số \(y=\dfrac{2}{3}x\) và \(y=x^2-x+\dfrac{2}{3}\)
Tìm tọa độ giao điểm của hai hàm số bằng phép tính
PTHĐGĐ của hai hs:
\(\dfrac{2}{3}x=x^2-x+\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{2}{3}\end{matrix}\right.\)
Thay x vào hàm số đầu tiên: \(\left[{}\begin{matrix}y=\dfrac{2}{3}\cdot1=\dfrac{2}{3}\\y=\dfrac{2}{3}\cdot\dfrac{2}{3}=\dfrac{4}{9}\end{matrix}\right.\)
Vậy hai hs cắt nhau tại: \(\left[{}\begin{matrix}A\left(1;\dfrac{2}{3}\right)\\A\left(\dfrac{2}{3};\dfrac{4}{9}\right)\end{matrix}\right.\)
Bài 1: Cho hàm số y=ax^2
a) Xác định a biết đồ thị của hàm số đi qua A(3;3)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a
c) Tìm điểm thuộc đồ thị có tung độ bằng 1
Bài 2: Cho hai hàm số: y=x^2 (P) và y=2x (d)
a) vẽ đồ thị (P) và (d) của hai hàm số trên cùng một hệ trục tọa độ
b) Tìm tọa độ gioa điểm của (P) và (d)
Bài 3: Cho hai hàm số y= (m+1)x^2 và y= 2x-1.
Tìm m biết rằng đồ thị của hai hàm số cắt nhau tại điểm có hoành độ bằng 2
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
Hàm số \(y = f\left( x \right) + g\left( x \right)\) có liên tục tại \(x = 2\) không? Giải thích.
Đặt \(h\left( x \right) = f\left( x \right) + g\left( x \right) = \frac{1}{{x - 1}} + \sqrt {4 - x} \). Ta có:
\(\begin{array}{l}h\left( 2 \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \\\mathop {\lim }\limits_{x \to 2} h\left( x \right) = \mathop {\lim }\limits_{x \to x} \left( {\frac{1}{{x - 1}} + \sqrt {4 - x} } \right) = \frac{1}{{2 - 1}} + \sqrt {4 - 2} = 1 + \sqrt 2 \end{array}\)
Vì \(\mathop {\lim }\limits_{x \to 2} h\left( x \right) = h\left( 2 \right)\) nên hàm số \(y = f\left( x \right) + g\left( x \right)\) liên tục tại \(x = 2\).