Cho dãy số (un) được xác định như sau: u 1 = 1 u n = 3 u n - 1 + 1 2 u n - 1 - 2 , n ≥ 2 Viết 4 số hạng đầu của dãy và chứng minh rằng un > 0, ∀ n
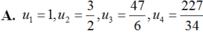
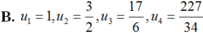
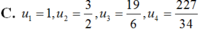
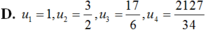
Cho dãy số (un) được xác định như sau: u1= 2017; un-1= n2(un-1 - un) với mọi n ∈ N*, n ≥2. Tìm giới hạn dãy số (un)
Lời giải:
$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.
Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$
Mặt khác:
$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.
Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$.
Ta có: $a=n^2(a-a)\Rightarrow a=0$
Vậy $\lim u_n=0$
Cho dãy số ( u n ) được xác định như sau u 1 = 2019 ; u n + 1 = u n 2 + 1 .Khi đó u 10 bằng ( làm tròn đến bốn số thập phân sau dấu phẩy)
A. 45,0333
B. 45,0222
C. 45,0444
D. 45, 0555
Cho dãy số u n được xác định như sau:
u 1 > 0 u n + 1 = u n u n 2 + 3 3 u n 2 + 1
Tùy thuộc vào giá trị của u 1 , tìm khẳng định ĐÚNG khi nói về tính tăng, giảm và bị chặn của dãy u n ?
A. Với mọi u 1 > 0 thì dãy u n luôn bị chặn
B. Nếu u 1 < 1 thì dãy u n giảm
C. Nếu u 1 > 1 thì dãy u n tăng
D. Nếu u 1 = 1 thì dãy u n là tăng
Cho dãy số (un) xác định như sau: u1= 2; un+1 - un - 2 + 2(4un+1 - \(\sqrt{4u_n+1}\)) = 0, ∀n∈ N*. Tìm số hạng tổng quát un của dãy số trên
Cho dãy số u n được xác định như sau: u 1 = 2 u n + 1 + 4 u n = 4 − 5 n n ≥ 1 . Tính tổng S = u 2018 − 2 u 2017 .
A. S = 2015 − 3.4 2017
B. S = 2016 − 3.4 2018
C. S = 2016 + 3.4 2018
D. S = 2015 + 3.4 2017
Đáp án A
Ta có:
u n + 1 + 4 u n = 4 − 5 n ⇔ u n + 1 = − 4 u n − 5 n + 4 ⇔ u n + 1 + n = − 4 u n + n − 1 * .
Đặt v n + 1 = u n + 1 + n suy ra v n = u n + n − 1 , khi đó * ⇔ v n + 1 = − 4 v n
Do đó v n là cấp số nhân với công bội q = − 4 ⇒ v n = − 4 n − 1 v 1
Mà v 1 = u 1 = 2 nên suy ra v n = 2. − 4 n − 1 → u n = 2. − 4 n − 1 − n + 1
Vậy:
S = u 2018 − 2 u 2017 = 2. − 4 2017 − 2017 − 2 2. − 4 2016 − 2016 = 2015 − 3.4 2017 .
Cho dãy số u n được xác định như sau u 1 = 2 u n + 1 + 4 u n = 4 - 5 n n ≥ 1 . Tính tổng S = u 2018 - 2 u 2017
A. S = 2015 - 3 . 4 2017
B. S = 2016 - 3 . 4 2017
C. S = 2017 + 3 . 4 2017
D. S = 2018 + 3 . 4 2017
Chọn A.
Phương pháp:
Cách giải: Ta có:
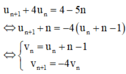

Cho dãy số u n được xác định như sau: u 1 = 2 u n + 1 + 4 u n = 4 − 5 n n ≥ 1 .
Tính tổng S = u 2018 − 2 u 2017 .
A. S = 2015 − 3.4 2017
B. S = 2016 − 3.4 2018
C. S = 2016 + 3.4 2018
D. S = 2015 + 3.4 2017
Cho dãy số ( u n ) được xác định như sau u 1 = 2 u n + 1 + 4 u n = 4 - 5 n .Tính tổng S = u 2018 - 2 u 2017
A. S = 2015 - 3 . 4 2017
B. S = 2016 - 3 . 4 2017
C. S = 2017 + 3 . 4 2017
D. S = 2018 + 3 . 4 2017
Chọn A
Phương pháp:
Cách giải: Ta có:
u n + 1 = n = - 4 ( u n + n - 1 )
⇔ u n + 1 + n = - 4 ( u n + n - 1 )
⇔ v n = u n + n - 1 v n + 1 = - 4 v n
Dãy ( v n ) là cấp số nhân với công bội -4 và v 1 = u 1 + 0 = 2
S = u 2018 - 2 u 2017
= v 2018 - 2 v 2017 + 2015
= 2015 - 3 . 4 2017
Cho dãy ( x k ) được xác định như sau:
x k = 1 2 ! + 2 3 ! + ... + k k + 1 ! . Tìm lim u n với
u n = x 1 n + x 2 n + ... + x 2017 n n
A. +∞
B. -∞
C. 1 − 1 2017 !
D. 1 + 1 2017 !