Tìm giới hạn E = lim x → 0 1 - sin π 2 cos x sin ( tan x )
A. +∞
B. -∞
C. 1
D. 0
Tính giới hạn hàm số :
\(\lim\limits_{x\rightarrow0}\frac{e^x-e^{-x}}{\sin x}\)
\(L=\lim\limits_{x\rightarrow0}\frac{e^x-e^{-x}}{\sin x}=\lim\limits_{x\rightarrow0}\frac{e^x-\frac{1}{e^x}}{\sin x}=\lim\limits_{x\rightarrow0}\frac{e^{2x}-1}{e^x\sin x}=\lim\limits_{x\rightarrow0}\frac{e^{2x}-1}{2x.\frac{\sin x}{2x}.e^x}\)
\(=\lim\limits_{x\rightarrow0}\frac{e^{2x}-1}{2x}.\frac{1}{\frac{\sin x}{x}}.\frac{2}{e^x}=1.\frac{1}{1}.\frac{2}{1}=2\)
a) Với \(h \ne 0,\) biến đổi hiệu \(\sin \left( {x + h} \right) - \sin x\) thành tích.
b) Sử dụng công thức giới hạn \(\mathop {\lim }\limits_{h \to 0} \frac{{\sin h}}{h} = 1\) và kết quả của câu a, tính đạo hàm của hàm số y = sin x tại điểm x bằng định nghĩa.
a) \(\sin \left( {x + h} \right) - \sin x = 2\cos \frac{{2x + h}}{2}.\sin \frac{h}{2}\)
b) Với \({x_0}\) bất kì, ta có:
\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin x - \sin {x_0}}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{2\cos \frac{{x + {x_0}}}{2}.\sin \frac{{x - {x_0}}}{2}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\sin \frac{{x - {x_0}}}{2}}}{{\frac{{x - {x_0}}}{2}}}.\mathop {\lim }\limits_{x \to {x_0}} \cos \frac{{x + {x_0}}}{2} = \cos {x_0}\end{array}\)
Vậy hàm số y = sin x có đạo hàm là hàm số \(y' = \cos x\)
a) Sử dụng phép đổi biến \(t = \frac{1}{x},\) tìm giới hạn \(\mathop {\lim }\limits_{x \to 0} {\left( {1 + x} \right)^{\frac{1}{x}}}.\)
b) Với \(y = {\left( {1 + x} \right)^{\frac{1}{x}}},\) tính ln y và tìm giới hạn của \(\mathop {\lim }\limits_{x \to 0} \ln y.\)
c) Đặt \(t = {e^x} - 1.\) Tính x theo t và tìm giới hạn \(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x}.\)
a) Ta có \(t = \frac{1}{x},\) nên khi x tiến đến 0 thì t tiến đến dương vô cùng do đó
\(\mathop {\lim }\limits_{x \to 0} {\left( {1 + x} \right)^{\frac{1}{x}}} = \mathop {\lim }\limits_{t \to + \infty } {\left( {1 + \frac{1}{t}} \right)^t} = e\)
b) \(\ln y = \ln {\left( {1 + x} \right)^{\frac{1}{x}}} = \frac{1}{x}\ln \left( {1 + x} \right)\)
\(\mathop {\lim }\limits_{x \to 0} \ln y = \mathop {\lim }\limits_{x \to 0} \frac{{\ln \left( {1 + x} \right)}}{x} = 1\)
c) \(t = {e^x} - 1 \Leftrightarrow {e^x} = t + 1 \Leftrightarrow x = \ln \left( {t + 1} \right)\)
\(\mathop {\lim }\limits_{x \to 0} \frac{{{e^x} - 1}}{x} = \mathop {\lim }\limits_{t \to 0} \frac{t}{{\ln \left( {t + 1} \right)}} = 1\)
Tìm giới hạn : \(L=\lim\limits_{x\rightarrow0}\frac{\sqrt[4]{\cos x}-\sqrt[5]{\cos x}}{\sin^2x}\)
Đổi biến \(\cos x=y^{20}\). Khi \(x\rightarrow0\) thì \(y\rightarrow0\). Ta có :
\(L=\lim\limits_{y\rightarrow0}\frac{y^5-y^4}{1-y^{40}}=-\lim\limits_{y\rightarrow0}\frac{y^4\left(y-1\right)}{y^{40}-1}\)
\(=-\lim\limits_{y\rightarrow0}\frac{y-1}{\left(y-1\right)\left(y^{39}+y^{38}+.....+y+1\right)}=-\frac{1}{40}\)
Tính các giới hạn
a) \(\lim\limits_{x\rightarrow a}\dfrac{\sin x-\sin a}{x-a}\)
b) \(\lim\limits_{x\rightarrow1}\left(1-x\right)\tan\dfrac{\pi x}{2}\)
c) \(\lim\limits_{x\rightarrow\dfrac{\pi}{3}}\dfrac{2\sin^2x+\sin x-1}{2\sin^2x-3\sin x+1}\)
d) \(\lim\limits_{x\rightarrow0}\dfrac{\tan x-\sin x}{\sin^3x}\)
tìm giới hạn
\(\lim\limits_{x\rightarrow1}\frac{1+sin\pi x}{x+1}\)
Lời giải:
\(\lim\limits_{x\to1}\frac{1+\sin\pi x}{x+1}=\frac{1+\sin\pi}{1+1}=\frac{1}{2}\)
Tìm giới hạn hàm số Lim x->4 1-x/(x-4)^2 Lim x->3+ 2x-1/x-3 Lim x->2+ -2x+1/x+2 Lim x->1- 3x-1/x+1
1: \(\lim\limits_{x\rightarrow4}\dfrac{1-x}{\left(x-4\right)^2}=-\infty\)
vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow4}1-x=1-4=-3< 0\\\lim\limits_{x\rightarrow4}\left(x-4\right)^2=\left(4-4\right)^2=0\end{matrix}\right.\)
2: \(\lim\limits_{x\rightarrow3^+}\dfrac{2x-1}{x-3}=+\infty\)
vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow3^+}2x-1=2\cdot3-1=5>0\\\lim\limits_{x\rightarrow3^+}x-3=3-3>0\end{matrix}\right.\) và x-3>0
3: \(\lim\limits_{x\rightarrow2^+}\dfrac{-2x+1}{x+2}\)
\(=\dfrac{-2\cdot2+1}{2+2}=\dfrac{-3}{4}\)
4: \(\lim\limits_{x\rightarrow1^-}\dfrac{3x-1}{x+1}=\dfrac{3\cdot1-1}{1+1}=\dfrac{2}{2}=1\)
a) Sử dụng giới hạn \(\mathop {\lim }\limits_{h \to 0} \frac{{{e^h} - 1}}{h} = 1\) và đẳng thức \({e^{x + h}} - {e^x} = {e^x}\left( {{e^h} - 1} \right),\) tính đạo hàm của hàm số \(y = {e^x}\) tại x bằng định nghĩa.
b) Sử dụng đẳng thức \({a^x} = {e^{x\ln a}}\,\,\left( {0 < a \ne 1} \right),\) hãy tính đạo hàm của hàm số \(y = {a^x}.\)
a) Với x bất kì và \(h = x - {x_0}\), ta có:
\(\begin{array}{l}f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{h \to 0} \frac{{f\left( {{x_0} + h} \right) - f\left( {{x_0}} \right)}}{h} = \mathop {\lim }\limits_{h \to 0} \frac{{{e^{{x_0} + h}} - {e^{{x_0}}}}}{h}\\ = \mathop {\lim }\limits_{h \to 0} \frac{{{e^{{x_o}}}\left( {{e^h} - 1} \right)}}{h} = \mathop {\lim }\limits_{h \to 0} {e^{{x_0}}}.\mathop {\lim }\limits_{h \to 0} \frac{{{e^h} - 1}}{h} = {e^{{x_0}}}\end{array}\)
Vậy hàm số \(y = {e^x}\) có đạo hàm là hàm số \(y' = {e^x}\)
b) Ta có \({a^x} = {e^{x\ln a}}\,\)nên \(\left( {{a^x}} \right)' = \left( {{e^{x\ln a}}} \right)' = \left( {x\ln a} \right)'.{e^{x\ln a}} = {e^{x\ln a}}\ln a = {a^x}\ln a\)
Bài 1. Tìm các giới hạn sau:
a) \(\lim\limits\dfrac{-2n+1}{n}\)
b) \(\lim\limits_{x\rightarrow1}\dfrac{3-\sqrt{x+8}}{x-1}\)
a) \(lim\dfrac{-2n+1}{n}=lim\dfrac{\dfrac{-2n}{n}+\dfrac{1}{n}}{\dfrac{n}{n}}=lim\dfrac{-2+\dfrac{1}{n}}{1}=\dfrac{lim\left(-2\right)+\dfrac{lim1}{n}}{lim1}=\dfrac{-2+0}{1}=-\dfrac{2}{1}=-2\)
b) \(\lim\limits_{x\rightarrow1}\dfrac{3-\sqrt{x+8}}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{9-\left(x+8\right)}{\left(x-1\right)\left(3+\sqrt{x+8}\right)}=\lim\limits_{x\rightarrow1}\dfrac{x-1}{\left(x-1\right)\left(3+\sqrt{x+8}\right)}=\lim\limits_{x\rightarrow1}\dfrac{1}{3+\sqrt{x+8}}=\dfrac{1}{3+\sqrt{1+8}}=\dfrac{1}{3+3}=\dfrac{1}{9}\)
Tìm giới hạn A = lim x → 0 1 - cos 2 x 2 sin 3 x 2 .
A. + ∞
B. - ∞
C. 1
D. 0
Ta có: 1 - c o s 2 x = 2 s i n 2 x nên:
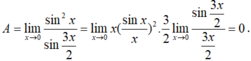
Chọn D.