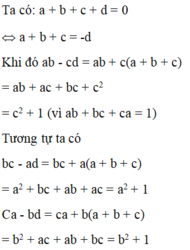cho ab - ac + bc - c2 = -1 với a;b;c E Z . khi đó a+b=
PT
Những câu hỏi liên quan
cho a,b,c thuộcz ab-ac+bc-c2=-1 chú ý c2 là mũ 2
Cho biết [a+b+c]2 \(=\) a2 + b2 + c2.CMR :
bc/a2 + ac/a2 +ab/c2 \(=\) 3
\(\left(a+b+c\right)^2=a^2+b^2+c^2\Leftrightarrow ab+bc+ca=0\)
\(\Rightarrow a^3b^3+b^3c^3+c^3a^3=3a^2b^2c^2\)
Ta có:
\(\dfrac{bc}{a^2}+\dfrac{ac}{b^2}+\dfrac{ab}{c^2}=\dfrac{a^3b^3+b^3c^3+c^3a^3}{a^2b^2c^2}=\dfrac{3a^2b^2c^2}{a^2b^2c^2}=3\)
Đúng 1
Bình luận (0)
Cho a, b, c, d thỏa mãn a + b + c + d 0; ab + ac + bc 1. Rút gọn biểu thức P
3(ab
−
cd)(bc
−
ad)(ca
−
bd)
(a
2
+
1)(b
2
+
1)(c
2
+...
Đọc tiếp
Cho a, b, c, d thỏa mãn a + b + c + d = 0; ab + ac + bc = 1. Rút gọn biểu thức P = 3(ab − cd)(bc − ad)(ca − bd) (a 2 + 1)(b 2 + 1)(c 2 + 1) ?
A. -1
B. 1
C. 3
D. -3
Cho ab + bc + ac = 9 , a≥1 , b≥1 , c≥1
tìm min và max của bt P = a2+b2+c2
Cho a,b,c ∈ Z thoả mãn ab - ac + bc - c2 = -1. Tính giá trị biểu thức M a+ b
\(ab-ac+bc-c^2=-1\)
<=> \(a\left(b-c\right)+c\left(b-c\right)=-1\)
<=> \(\left(a+c\right)\left(b-c\right)=-1\)
Mà \(a,b,c\in Z\Rightarrow\left\{{}\begin{matrix}a+c\in Z\\b-c\in Z\end{matrix}\right.\)
- Nếu \(\left\{{}\begin{matrix}a+c=1\\b-c=-1\end{matrix}\right.\) => a + b = 0
- Nếu \(\left\{{}\begin{matrix}a+c=-1\\b-c=1\end{matrix}\right.\) => a + b = 0
Vậy M = 0
Đúng 3
Bình luận (1)
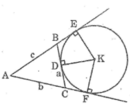
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC a, AC b, AB c. Chứng minh rằng:
B
E
a
+
b
-
c
2
Đọc tiếp
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, AC = b, AB = c. Chứng minh rằng: B E = a + b - c 2
Ta có: B E = A E - A B = a + b + c 2 - c = a + b - c 2
Đúng 0
Bình luận (0)
1,Cho các số thực a,b,c thỏa mãn điều kiện : a2+b2+c2=3a2+b2+c2=3 và a+b+c+ab+ac+bc=6a+b+c+ab+ac+bc=6.
Tính A=a30+b4+c1975a30+b4+c2014
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC a, AC b, AB c. Chứng minh rằng:
A
E
A
F
a
+
b
+
c
2
Đọc tiếp
Cho tam giác ABC, đường tròn (K) bàng tiếp trong góc A tiếp xúc với các tia AB và AC theo thứ tự tại E và F. Cho BC = a, AC = b, AB = c. Chứng minh rằng: A E = A F = a + b + c 2

Gọi D là tiếp điểm của đường tròn (K) với cạnh BC.
Theo tính chất hai tiếp tuyến cắt nhau ta có:
BE = BD; CD = CF
AE = AB + BE
AF = AC + CF
Suy ra: AE + AF = AB + BE + AC + CF
= AB + AC + (BD + DC)
= AB + AC + BC = c + b + a
Mà: AE = AF (tính chất hai tiếp tuyến cắt nhau)
Suy ra: A E = A F = a + b + c 2
Đúng 0
Bình luận (0)
cho a, b,c >0 thỏa mãn ab+bc+ca=abc
CMR : (√b2+2a2)/ab + (√c2+2b2)/bc + (√a2+2c2)/ac