Cho lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi có độ dài cạnh 3cm, góc ∠ A B C = 60 o và chiều cao AA’ của hình lăng trụ bằng 4cm. Tính:
a) Diện tích xung quanh của hình lăng trụ.
b) Thể tích của hình lăng trụ đó.
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi, cạnh a; \(\widehat{BAD}=60^0\). Biết \(AB'\perp BD'\). Tính thể tích khối lăng trụ \(\left(V=S_đ.h\right)\)
Đặt \(x=AA'\)
Ta có: \(\overrightarrow{AB'}=\overrightarrow{AA'}+\overrightarrow{AB}\) ; \(\overrightarrow{BD'}=\overrightarrow{BB'}+\overrightarrow{BD}=\overrightarrow{BB'}+\overrightarrow{BA}+\overrightarrow{BC}=\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{AB'}.\overrightarrow{BD'}=\left(\overrightarrow{AA'}+\overrightarrow{AB}\right)\left(\overrightarrow{AA'}-\overrightarrow{AB}+\overrightarrow{BC}\right)\)
\(=AA'^2+\overrightarrow{AA'}\left(-\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{AB}.\overrightarrow{AA'}-AB^2+\overrightarrow{AB}.\overrightarrow{BC}\)
\(=x^2-a^2+AB.BC.cos120^0\)
\(=x^2-a^2-\dfrac{a^2}{2}=x^2-\dfrac{3a^2}{2}=0\)
\(\Rightarrow x=\dfrac{a\sqrt{6}}{2}\)
\(V=\dfrac{a\sqrt{6}}{2}.2.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{2}}{4}\)
Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy là hình vuông cạnh bằng 4cm, đường chéo AB′ của mặt bên (ABB′A′) có độ dài bằng 5cm. Tính thể tích V của khối lăng trụ ABCD.A′B′C′D′.
A. 48 cm 3
B. 24 cm 3
C. 16 cm 3
D. 32 cm 3
tính sxq , stp của lăng trụ đứng tứ giác có đáy là hình thoi cạnh a hai đườngcheos m,n độ dài cạnh bên của hình lăng trụ là c
tính sxq , stp của lăng trụ đứng tứ giác có đáy là hình thoi cạnh a hai đườngcheos m,n độ dài cạnh bên của hình lăng trụ là c
Chu vi đáy của hình lăn trụ là:
\(a+a+a+a=4a\)
Diện tích xung quanh của hình lăn trụ là:
\(S_{xq}=2p\cdot h=4a\cdot c=4ac\)
Diện tích đáy của hình lăn trụ đứng:
\(S_{\text{đ}}=\dfrac{d_1\cdot d_2}{2}=\dfrac{m\cdot n}{2}\)
Diện tích toàn phần của hình lăn trụ:
\(S_{tp}=S_{xq}+2S_{\text{đ}}\)
\(\Rightarrow S_{tp}=4ac+2\cdot\dfrac{m\cdot n}{2}=4ac+m\cdot n\)
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là một hình thoi cạnh a, góc BAD= 60 o Gọi M là trung điểm AA' và N là trung điểm của CC' Chứng minh rằng bốn điểm B', M, N, D đồng phẳng. Hãy tính độ dài cạnh AA' theo a để tứ giác B'MDN là hình vuông.
A. a 2
B. a
C. a 2 2
D. a 3
Cho hình lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là một hình thoi cạnh a, góc BAD ^ = 60 ° . Gọi M là trung điểm AA' và N là trung điểm của CC' Chứng minh rằng bốn điểm B', M, N, D đồng phẳng. Hãy tính độ dài cạnh AA' theo a để tứ giác B'MDN là hình vuông.
A. a 2
B. a
C. a 2 2
D. a 3
Đáp án A
Gọi P là trung điểm cùa DD'
A'B'NP là hình bình hành => A'P // B'N
A'PDM là hình bình hành => A'P // MD
=> B'N // MD hay B' M, N, D đồng phẳng.
Tứ giác B'NDM là hình bình hành.
Có DM = B'M nên B'NDM là hình thoi.

cho lăng trụ đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi cạnh bằng a, góc ABC =60 độ, AA'= 3a. tính thể tích khối lăng trụ đó
Gọi O là tâm hình thoi ABCD.
Do ABCD là hình thoi mà \(\widehat{ABC}=60^o\)
⇒ Tam giác ABC đều.
⇒ \(BO=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
⇒ \(BD=2BO=a\sqrt{3}\)
\(V_{ABCD.A'B'C'D'}=AA'\cdot S_{ABCD}=3a\cdot\dfrac{1}{2}\cdot a\sqrt{3}\cdot a=\dfrac{3a\sqrt{3}}{2}\)
Một hình lăng trụ đứng ABC.DEF có đáy là một tam giác vuông, chiều cao của lăng trụ là 9 cm. Độ dài 2 cạnh góc vuông của đáy là 3cm và 4 cm (Hình vẽ).
a) Tính độ dài cạnh BC.
b) Tính diện tích xung quanh của hình lăng trụ đứng.
c) Tính diện tích toàn phần của hình lăng trụ đứng.
d) Tính thể tích của hình lăng trụ đứng.
Cho hình lăng trụ đứng ABCD. 'D ' có ABCD là hình thoi cạnh a, góc giữa đường thẳng A 'B và mặt phẳng (ABCD) bằng 600 . Tính khoảng cách d giữa hai đường thẳng AC và B ' D '
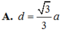
![]()
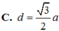
![]()