Đồ thị hàm số y = ax + b x − 1 cắt trục tung tại điểm A(0;−1), tiếp tuyến của đồ thị tại điểm A có hệ số góc k = - 3 . Giá trị của của thức P=a+b là
A. 1
B. 3
C. 4
D. 2
Bài 9: Xác định hàm số y= ax+b biÕt
a) Đồ thị của hàm số qua A(1;-1) và có hệ số góc là 2
b) Đồ thị của hàm số // với đường thẳng y =-3x + 2 và cắt trục tung tại điểm có tung độ bằng 1.
Bài 10: Cho hàm số: y = -x + 2.
a) Vẽ đồ thị của hàm số trên.
b)Gọi A, B là giao điểm của đồ thị hàm số với các trục tọa độ. Tính khoảng cách từ gốc tọa độ O đến đường thẳng AB.
Bài 10:
a: 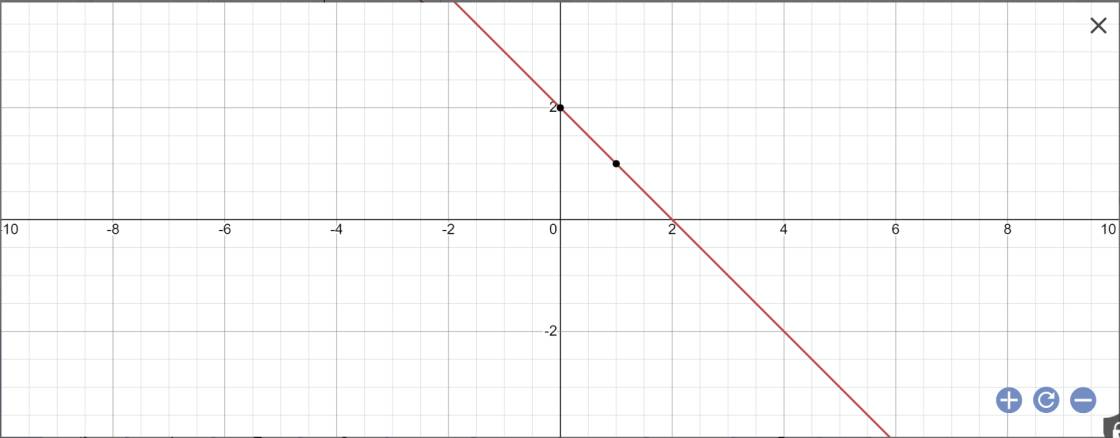
b:
y=-x+2
=>y+x-2=0
=>x+y-2=0
Khoảng cách từ O đến đến đường thẳng AB sẽ bằng khoảng cách từ O đến (d): y=-x+2
=>Khoảng cách từ O đến đường thẳng AB là:
\(d\left(O;\left(d\right)\right)=\dfrac{\left|0\cdot1+0\cdot1+\left(-2\right)\right|}{\sqrt{1^2+1^2}}=\dfrac{2}{\sqrt{2}}=\sqrt{2}\)
Bài 9:
a: Vì hệ số góc của hàm số y=ax+b là 2 nên a=2
=>y=2x+b
Thay x=1 và y=-1 vào y=2x+b, ta được:
\(b+2\cdot1=-1\)
=>b+2=-1
=>b=-3
vậy: y=2x-3
b: Vì đồ thị của hàm số y=ax+b song song với đường thẳng y=-3x+2 nên \(\left\{{}\begin{matrix}a=-3\\b\ne2\end{matrix}\right.\)
Vậy: y=-3x+b
Thay x=0 và y=1 vào y=-3x+b, ta được:
\(b-3\cdot0=1\)
=>b-0=1
=>b=1
Vậy: y=-3x+1
Bài 9:
a. Hệ số góc của đths là $2$, tức $a=2$
ĐTHS đi qua điểm $A(1;-1)$ nên:
$-1=a.1+b$
$\Leftrightarrow -1=2.1+b\Rightarrow b=-3$
Vậy hàm số cần tìm là $y=2x-3$
b.
ĐTHS song song với $y=-3x+2$ nên $a=-3$
ĐTHS cần tìm cắt trục tung tại điểm có tung độ $1$, tức là nó đi qua điểm $(0;1)$
$\Rightarrow 1=a.0+b\Rightarrow b=1$
Vậy đths cần tìm là $y=-3x+1$
Bài 10:
a. Bạn chọn 2 điểm bất kỳ thuộc ĐTHS và nối lại sẽ được đồ thị hàm số cần tìm.
b.
$A\in Ox\Rightarrow y_A=0$
Có: $0=y_A=-x_A+2\Rightarrow x_A=2$. Vậy điểm $A$ có tọa độ $(2;0)$
$B\in Oy\Rightarrow x_B=0$
$y_B=-x_B+2=-0+2=2$. Vậy điểm $B$ có tọa độ $(0;2)$
Gọi $d$ là khoảng cách từ $O$ đến $AB$. Theo công thức hệ thức lượng trong tam giác vuông:
$\frac{1}{d^2}=\frac{1}{OA^2}+\frac{1}{OB^2}=\frac{1}{|x_A|^2}+\frac{1}{|y_B|^2}$
$=\frac{1}{2^2}+\frac{1}{2^2}=\frac{1}{2}$
$\Rightarrow d=\sqrt{2}$
1) xác định đồ thị hàm số bậc nhất \(y=ax+b\) trong mỗi trường hợp sau:
a) đồ thị hàm số đi qua A(-1; 2), B(2; -3)
b) đồ thị hàm số có hệ số góc là 2 và cắt trục tung tại điểm có tung độ là 2
c) đồ thị hàm số tạo với trục hoành 1 góc \(60^0\) và đi qua điểm B(1; -3)
giúp mk vs ah mk cần gấp
xác định hàm số y= ax+b biết:
a) khi a=3, đồ thị hàm số cắt trục hoành tại điểm có hoành độ =\(\sqrt{2}\)
b) khi a=-3, đò thị hàm số cắt trục tung tại điểm có tung độ = 5
c) đồ thị hàm số đi qua điểm A (-1,-2) song song vớ đường thẳng y=-1-x
Cho hàm số y = –2x + 3 có đồ thị (d1) và hàm số y = x – 1 có đồ thị ( d 2 )
b) Xác định hệ số a và b biết đường thẳng ( d 3 ): y = ax + b song song với ( d 2 ) và cắt ( d 1 ) tại điểm nằm trên trục tung.
b) Do ( d 3 ) song song với đường thẳng ( d 2 ) nên ( d 3 ) có dạng: y = x + b (b ≠ -1)
( d 1 ) cắt trục tung tại điểm (0; 3)
Do ( d 3 ) cắt ( d 1 ) tại điểm nằm trên trục tung nên ta có:
3 = 0 + b ⇔ b = 3
Vậy phương trình đường thẳng ( d 3 ) là y = x + 3
Cho hàm số y = f(x) = a x + b c x + d ( a,b,c,d ∈ ℝ , - d c ≠ 0) đồ thị hàm số y= f’(x) như hình vẽ.

Biết đồ thị hàm số y= f(x) cắt trục tung tại điểm có tung độ bằng 3. Tìm phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành ?
A. y = x - 3 x + 1
B. y = x + 3 x - 1
C. y = x + 3 x + 1
D. y = x - 3 x - 1
+ Ta có y ' = f ' ( x ) = a d - b c ( c x + d ) 2 . Từ đồ thị hàm số y= f’(x) ta thấy:
Đồ thị hàm số y= f’(x) có tiệm cận đứng x=1 nên –d/c= 1 hay c= -d
Đồ thị hàm số y= f’(x ) đi qua điểm (2;2)
⇒ a d - b c ( 2 c + d ) 2 = 2 ↔ a d - b c = 2 ( 2 c + d ) 2
Đồ thị hàm số y= f’(x) đi qua điểm (0;2)
⇒ a d - b c d 2 = 2 ↔ a d - b c = 2 d 2
Đồ thị hàm số y=f(x) đi qua điểm (0;3) nên b/d= 3 hay b= 3d
Giải hệ gồm 4 pt này ta được a=c= -d và b= 3d .
Ta chọn a=c= 1 ; b= -3 ; d= -1
⇒ y = x - 3 x - 1
Chọn D.
Bài 1: Cho hàm số y=\(-\)ax+5. Hãy xác định hệ số a biết rằng:
a, Đồ thị hàm số song song với đường thẳng y=3x
b, Khi x=1+\(\sqrt{3}\) thì y=\(4-\sqrt{3}\)
Bài 2: Cho hàm số y=3x+b. Hãy xác định hệ số b trong mỗi trường hợp sau:
a, Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng \(-3\)
b, Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(-4\)
c, Đồ thị hàm số đi qua điểm M(\(-1;2\))
Mong mọi người giúp đỡ vì mình cần gấp ạ
2:
a: Thay x=0 và y=-3 vào (d), ta được:
3*0+b=-3
=>b=-3
b: Thay x=-4 và y=0 vào (d), ta được:
3*(-4)+b=0
=>b=12
c: Thay x=-1 và y=2 vào (d), ta được:
3*(-1)+b=2
=>b-3=2
=>b=5
Cho hàm số y = ax + b . Xđ hàm số biết đồ thị của nó cắt trục tung tại điểm có tung độ = -1 và song song với đường thẳng y = \(\dfrac{2}{3}x+1\)
Vì đồ thị hàm số y=ax+b song song với đường thẳng \(y=\dfrac{2}{3}x+1\) nên \(\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b\ne1\end{matrix}\right.\)
hay hàm số có dạng là \(y=\dfrac{2}{3}x+b\)
Vì đồ thị hàm số \(y=\dfrac{2}{3}x+b\) cắt trục tung tại điểm có tung độ bằng -1 nên
Thay x=0 và y=-1 vào hàm số \(y=\dfrac{2}{3}x+b\), ta được:
\(\dfrac{2}{3}\cdot0+b=-1\)
\(\Leftrightarrow b=-1\)
Vậy: Hàm số có dạng là \(y=\dfrac{2}{3}x-1\)
- Thấy đường thẳng song song với \(y=\dfrac{2}{3}x+1\)
\(\Rightarrow\left\{{}\begin{matrix}a=a^,\\b\ne b^,\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\b\ne1\end{matrix}\right.\)
=> Phương trình đường thẳng có dạng : \(y=\dfrac{2}{3}x+b\)
Lại có đồ thị cắt trục tung tại điểm có tung độ là - 1
=> b = -1 ( TM )
Vậy phương trình đường thẳng cần tìm có dạng : \(y=\dfrac{2}{3}x-1\)
cho hàm số y = x2
a/. Vẽ đồ thị hàm số
b/ .Xác định cac1 số a và b sao cho đường thẳng y = ax+ b cắt trục tung tại điểm có tung độ bằng 2 và cắt đồ thị hàm số đã cho tại điểm có hoành độ bằng 1
Bài 1. Xác định hàm số y = ax + b biết
a) Đồ thị hàm số cắt trục hoành tại điểm A có hoành độ -4 và cắt trục tung tại điểm B có tung độ 3.
b) Đồ thị của nó song song với đường thẳng y = 3x + 1 và đi qua điểm M(4; -5).
c) Đồ thị của nó là đường thẳng đi qua hai điểm M(3; 5) và N(-1; -7).
d) Đồ thị của nó là đường thẳng cắt đường thẳng y = 2x - 3 tại điểm C có hoành độ là 2 và đi qua điểm
A(3; -4).
e) Đồ thị của nó là đường thẳng đi qua điểm D(-2; 3) và tạo với trục Ox một góc 45◦.
Bài 1:
a: Theo đề, ta có:
\(\left\{{}\begin{matrix}-4a+b=0\\b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{3}{4}\\b=3\end{matrix}\right.\)
Cho hàm số bậc nhất y= ax +b có đồ thị đi qua M(1;4 ) .Đồ thị hàm số y=ax+b cắt trục Ox tại điểm P có hoành độ dương và cắt trục Oy tại Q có tung độ dương . Tìm a,b để OP+OQ nhỏ nhất ( với O là gốc tọa độ)