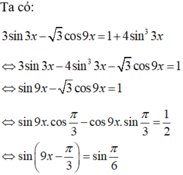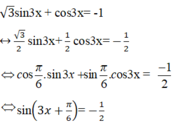Giải phương trình sau: 3sin3x - 4cos3x = 5
PB
Những câu hỏi liên quan
Giải các phương trình sau: a) cosx – √3sinx = √2; b) 3sin3x – 4cos3x = 5; c) 2sin2x + 2cos2x – √2 = 0; d) 5cos2x + 12sin2x -13 = 0.
a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).
Đúng 0
Bình luận (0)
Giá trị lớn nhất của hàm số y = 3sin3x-4cos3x+5 ?
A. 5
B.10
C.4
D.12
Đáp án B
3sin3x - 4cos3x ≤ 3 2 + ( - 4 ) 2 = 5 => Maxy 5 + 5 =10
Đúng 0
Bình luận (0)
Giá trị lớn nhất của hàm số y = 3sin3x - 4cos3x + 5 ?
A. 5
B. 10
C. 4
D. 12
Đáp án B
Ta có: 3 sin 3 x - 4 cos 3 x ≤ 3 2 + - 4 2 = 5 ⇒ M a x R y = 5 + 5 = 10 .
Đúng 0
Bình luận (0)
Giải các phương trình sau:
a) cosx - √3sinx = √2; b) 3sin3x - 4cos3x = 5;
b) 2sin2x + 2cos2x - √2 = 0; c) 5cos2x + 12sin2x -13 = 0.
a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 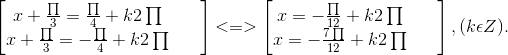
b) 3sin3x - 4cos3x = 5 ⇔ ![]() sin3x -
sin3x - ![]() cos3x = 1.
cos3x = 1.
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = ![]() + k2π
+ k2π
⇔ x = ![]() , k ∈ Z (trong đó α = arccos
, k ∈ Z (trong đó α = arccos![]() ).
).
c) Ta có sinx + cosx = √2cos(x - ![]() ) nên phương trình tương đương với
) nên phương trình tương đương với
2√2cos(x - ![]() ) - √2 = 0 ⇔ cos(x -
) - √2 = 0 ⇔ cos(x - ![]() ) =
) = ![]()
⇔ 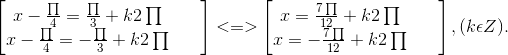
d) 5cos2x + 12sin2x -13 = 0 ⇔ ![]()
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαcos2x + sinαsin2x = 1 ⇔ cos(2x - α) = 1
⇔ x = ![]() + kπ, k ∈ Z (trong đó α = arccos
+ kπ, k ∈ Z (trong đó α = arccos![]() ).
).
Đúng 0
Bình luận (0)
Dương Hoàng Minh làm kiểu j mà 1 nấy bài trong 2p ?
Đúng 0
Bình luận (4)
Xem thêm câu trả lời
Câu 3 )
a) 2sinx + 2cosx -√2 = 0
b) 3sin3x - 4cos3x = 5
2 câu này cách làm y hệt vừa nãy thôi, ko có gì phức tạp cả :(
a/ \(\Leftrightarrow2\sin x+2\cos x=\sqrt{2}\)
\(\cos\frac{x}{2}=0\Rightarrow x=\pi+k2\pi\)
\(\cos x\ne0\Leftrightarrow x\ne\pi+k2\pi\)
Đặt \(t=\tan\frac{x}{2}\Rightarrow\left\{{}\begin{matrix}\sin x=\frac{2t}{1+t^2}\\\cos x=\frac{1-t^2}{1+t^2}\end{matrix}\right.\)
\(\Leftrightarrow2.\frac{2t}{1+t^2}+2.\frac{1-t^2}{1+t^2}=\sqrt{2}\)
\(\Leftrightarrow\left(\sqrt{2}+2\right)t^2-4t+\sqrt{2}-2=0\) <pt ẩn t bạn tự giải>
Câu dưới tương tự
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của hàm số
y
2
-
3
sin
3
x
+
4
cos
3
x
trên R. A.
m
a
x
R
y
7
B.
m
a
x
R
y
5
C. ...
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y = 2 - 3 sin 3 x + 4 cos 3 x trên R.
A. m a x R y = 7
B. m a x R y = 5
C. m a x R y = 9
D. m a x R y = 3
Tìm giá trị lớn nhất của hàm số y2-3sin3x+4cos3x trên R A. B. C. D.
Đọc tiếp
Tìm giá trị lớn nhất của hàm số y=2-3sin3x+4cos3x trên R
A.![]()
B. ![]()
C. ![]()
D. ![]()
Giải phương trình
3
sin
3
x
-
3
cos
9
x
1
+
4
sin
3
3
x
Đọc tiếp
Giải phương trình 3 sin 3 x - 3 cos 9 x = 1 + 4 sin 3 3 x
![]()
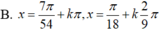
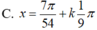
![]()
Phương trình
3
sin
3
x
+
cos
3
x
-
1
tương đương với phương trình nào sau đây? A.
sin
2
x
-
π
6
1
2
B.
sin
3
x
+...
Đọc tiếp
Phương trình 3 sin 3 x + cos 3 x = - 1 tương đương với phương trình nào sau đây?
A. sin 2 x - π 6 = 1 2
B. sin 3 x + π 6 = π 6
C. sin 3 x + π 6 = - 1 2
D. sin 3 x + π 6 = 1 2