a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 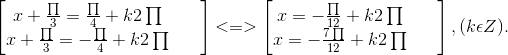
b) 3sin3x - 4cos3x = 5 ⇔ ![]() sin3x -
sin3x - ![]() cos3x = 1.
cos3x = 1.
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = ![]() + k2π
+ k2π
⇔ x = ![]() , k ∈ Z (trong đó α = arccos
, k ∈ Z (trong đó α = arccos![]() ).
).
c) Ta có sinx + cosx = √2cos(x - ![]() ) nên phương trình tương đương với
) nên phương trình tương đương với
2√2cos(x - ![]() ) - √2 = 0 ⇔ cos(x -
) - √2 = 0 ⇔ cos(x - ![]() ) =
) = ![]()
⇔ 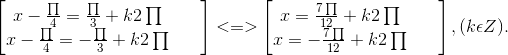
d) 5cos2x + 12sin2x -13 = 0 ⇔ ![]()
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαcos2x + sinαsin2x = 1 ⇔ cos(2x - α) = 1
⇔ x = ![]() + kπ, k ∈ Z (trong đó α = arccos
+ kπ, k ∈ Z (trong đó α = arccos![]() ).
).
Dương Hoàng Minh làm kiểu j mà 1 nấy bài trong 2p ?
a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5).

