Giải các phương trình sau:
a) x + 2 + 7 − 9 = 0 ; b) x 2 − 1 − 1 = 2 .
1.Giải các phương trình sau:
a) 2x2 +16 -6 = 4\(\sqrt{x\left(x+8\right)}\)
b) x4 -8x2 + x-2\(\sqrt{x-1}\) + 16=0
2. Gọi x1;x2 là nghiệm phương trình x2 -3x -7 =0. Không giải phương trình tính các giá trị của biểu thức sau:
A = \(\dfrac{1}{x_1-1}+\dfrac{1}{x_2-1}\)
B= \(x^2_1+x_2^2\)
C= |x1 - x2|
D= \(x_1^4+x_2^4\)
E= (3x1 + x2) (3x2 + x1)
2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1
giải các phương trình sau:
a, √ 16x - 2√ x + √ 9x = 12
b, √ (4x² - 12x + 9) = 7
b: \(\Leftrightarrow\left|2x-3\right|=7\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=7\\2x-3=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
\(a,ĐK:x\ge0\\ PT\Leftrightarrow4\sqrt{x}-2\sqrt{x}+3\sqrt{x}=12\\ \Leftrightarrow5\sqrt{x}=12\Leftrightarrow\sqrt{x}=\dfrac{12}{5}\\ \Leftrightarrow x=\dfrac{144}{25}\left(tm\right)\\ b,PT\Leftrightarrow\sqrt{\left(2x-3\right)^2}=7\Leftrightarrow\left|2x-3\right|=7\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=7\\3-2x=7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
Giải các phương trình sau:
a, \(|x^2-x+2|-3x-7=0\)
b, \(|x-1|+|2x+3|=|x|+4\)
a) Ta có: \(\left|x^2-x+2\right|-3x-7=0\)
\(\Leftrightarrow\left|x^2-x+2\right|=3x+7\)
\(\Leftrightarrow x^2-x+2=3x+7\)(Vì \(x^2-x+2>0\forall x\))
\(\Leftrightarrow x^2-x+2-3x-7=0\)
\(\Leftrightarrow x^2-4x-5=0\)
\(\Leftrightarrow x^2-5x+x-5=0\)
\(\Leftrightarrow x\left(x-5\right)+\left(x-5\right)=0\)
\(\Leftrightarrow\left(x-5\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)
Vậy: S={5;-1}
Giải các phương trình sau:
a) \(\dfrac{3}{x-7}+\dfrac{2}{x+7}=\dfrac{5}{x^2-49}\)
b) \(\dfrac{2x-1}{3}-\dfrac{x+3}{2}>1+\dfrac{5x}{6}\)
a) \(\dfrac{3}{x-7}+\dfrac{2}{x+7}=\dfrac{5}{x^2-49}\)
(ĐKXĐ: x khác 7; x khác -7)
<=>\(\dfrac{3.\left(x+7\right)}{\left(x-7\right).\left(x+7\right)}+\dfrac{2.\left(x-7\right)}{\left(x+7\right).\left(x-7\right)}=\dfrac{5}{\left(x+7\right).\left(x-7\right)}\)
=> 3x + 21 + 2x - 14 = 5
<=> 3x + 2x = 5 + 14 - 21
<=> 5x = -2
<=> x = \(\dfrac{-2}{5}\)
Vậy S = { \(\dfrac{-2}{5}\) }
b) \(\dfrac{2x-1}{3}-\dfrac{x+3}{2}>1+\dfrac{5x}{6}\)
<=> \(\dfrac{2.\left(2x-1\right)}{3.2}-\dfrac{3.\left(x+3\right)}{3.2}>\dfrac{1.6}{6}+\dfrac{5x}{6}\)
=> 4x - 2 - 3x - 9 > 6 + 5x
<=> 4x - 3x - 5x > 6 + 9 + 2
<=> -4x > 17
<=> \(\dfrac{-17}{4}\)
Vậy S = { \(\dfrac{-17}{4}\) }
Giải các phương trình sau:
a) \(\sqrt {3{x^2} - 6x + 1} = \sqrt { - 2{x^2} - 9x + 1} \)
b) \(\sqrt {2{x^2} - 3x - 5} = \sqrt {{x^2} - 7} \)
a) \(\sqrt {3{x^2} - 6x + 1} = \sqrt { - 2{x^2} - 9x + 1} \)
Bình phương hai vế của phương trình \(\sqrt {3{x^2} - 6x + 1} = \sqrt { - 2{x^2} - 9x + 1} \) ta được
\(3{x^2} - 6x + 1 = - 2{x^2} - 9x + 1\)
\( \Leftrightarrow 5{x^2} + 3x = 0\)
\( \Leftrightarrow x\left( {5x + 3} \right) = 0\)
\( \Leftrightarrow x = 0\) hoặc \(x = \frac{{ - 3}}{5}\)
Thay lần lượt hai giá trị này của x vào phương trình đã cho, ta thấy cả hai giá trị x = 0 và \(x = \frac{{ - 3}}{5}\) đều thỏa mãn.
Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ {0;\frac{{ - 3}}{5}} \right\}\)
b) \(\sqrt {2{x^2} - 3x - 5} = \sqrt {{x^2} - 7} \)
Bình phương hai vế của phương trình \(\sqrt {2{x^2} - 3x - 5} = \sqrt {{x^2} - 7} \) , ta được
\(2{x^2} - 3x - 5 = {x^2} - 7\)
\( \Leftrightarrow {x^2} - 3x + 2 = 0\)
\( \Leftrightarrow x = 1\) hoặc \(\)\(x = 2\)
Thay lần lượt giá trị của x vào phương trình đã cho, ta thấy không có giá trị nào của x thỏa mãn.
Vậy phương trình đã cho vô nghiệm.
Giải các bất phương trình sau:
a)\(\left|3x-2\right|>7\)
\(\left|3x-2\right|>7\)
\(\Leftrightarrow\left(3x-2\right)^2>49\)
\(\Leftrightarrow9x^2-12x-45>0\)
\(\Leftrightarrow\left(x-3\right)\left(3x+5\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x>3\\x< -\dfrac{5}{3}\end{matrix}\right.\)
Giải các hệ phương trình sau:
a.{1/x - 1/y = 1
{2/x - 3/y = 5
b.{15/x - 7/y = 9
{4/x + 9/y = 35
\(a,\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{2}{y}=2\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\left(x,y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{5}{y}=3\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{5}{3}\\\dfrac{2}{x}+\dfrac{9}{5}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{8}\\y=-\dfrac{5}{3}\end{matrix}\right.\)
\(b,\Leftrightarrow\left\{{}\begin{matrix}\dfrac{60}{x}-\dfrac{28}{y}=36\\\dfrac{60}{x}-\dfrac{135}{y}=525\end{matrix}\right.\left(x,y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{9}{y}=35\\-\dfrac{163}{y}=489\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}-27=35\\y=-\dfrac{1}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{31}\\y=-\dfrac{1}{3}\end{matrix}\right.\)
a: Ta có: \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=1\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{2}{y}=2\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=-3\\\dfrac{1}{x}-\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1}{3}\\\dfrac{1}{x}=1+\dfrac{1}{y}=1+\left(-3\right)=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{1}{3}\\x=\dfrac{-1}{2}\end{matrix}\right.\)
Giải các bất phương trình sau:
a) -2x2 + 7x - 10 < 0
b) \(\dfrac{1+x}{1-x}\) ≤ 2
c) \(\dfrac{x}{x-2}-\dfrac{2}{x-3}\) > 1
d) (x2 + 4x + 10)2 - 7(x2 + 4x + 11) + 7 < 0
Giải các bất phương trình sau:
a) \(7{x^2} - 19x - 6 \ge 0\)
b) \( - 6{x^2} + 11x > 10\)
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1\)
d) \({x^2} - 10x + 25 \le 0\)
a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau

Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
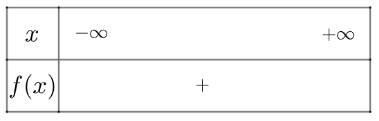
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau

Vậy nghiệm của bất phương trình là \(x = 5\)
Giải các bất phương trình sau:
a) \({\log _{\frac{1}{7}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right);\)
b) \(2\log \left( {2x + 1} \right) > 3.\)
a) \({\log _{\frac{1}{7}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\) (ĐK: \(x + 1 > 0;2 - x > 0 \Leftrightarrow - 1 < x < 2\))
\(\begin{array}{l} \Leftrightarrow {\log _{{7^{ - 1}}}}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow - {\log _7}\left( {x + 1} \right) > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\log _7}{\left( {x + 1} \right)^{ - 1}} > {\log _7}\left( {2 - x} \right)\\ \Leftrightarrow {\left( {x + 1} \right)^{ - 1}} > 2 - x\\ \Leftrightarrow \frac{1}{{x + 1}} - 2 + x > 0\\ \Leftrightarrow \frac{{1 + \left( {x - 2} \right)\left( {x + 1} \right)}}{{x + 1}} > 0\\ \Leftrightarrow \frac{{1 + {x^2} - x - 2}}{{x + 1}} > 0 \Leftrightarrow \frac{{{x^2} - x - 1}}{{x + 1}} > 0\end{array}\)
Mà – 1 < x < 2 nên x + 1 > 0
\( \Leftrightarrow {x^2} - x - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}x < \frac{{1 - \sqrt 5 }}{2}\\x > \frac{{1 + \sqrt 5 }}{2}\end{array} \right.\)
KHĐK ta có \(\left[ \begin{array}{l} - 1 < x < \frac{{1 - \sqrt 5 }}{2}\\\frac{{1 + \sqrt 5 }}{2} < x < 2\end{array} \right.\)
b) \(2\log \left( {2x + 1} \right) > 3\) (ĐK: \(2x + 1 > 0 \Leftrightarrow x > \frac{{ - 1}}{2}\))
\(\begin{array}{l} \Leftrightarrow \log \left( {2x + 1} \right) > \frac{3}{2}\\ \Leftrightarrow 2x + 1 > {10^{\frac{3}{2}}} = 10\sqrt {10} \\ \Leftrightarrow x > \frac{{10\sqrt {10} - 1}}{2}\end{array}\)
KHĐK ta có \(x > \frac{{10\sqrt {10} - 1}}{2}\)