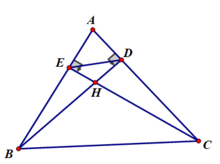
Cho tam giác ABC nhọn, các đường cao BD và CE cắt nhau tại H. Chứng minh
B C 2 = B H . B D + C H . C E .
C1. Cho tam giác nhọn DEF. Đường cao EA và FB cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C2. Cho tam giác nhọn ABC. Đường cao BD và CE cắt nhau tại H.
a) Chứng minh rằng
b) Chứng minh rằng
C3. Cho ABC vuông tại A, đư¬ờng cao AH cắt đ¬ường phân giác CD tại I.
a) Chứng minh rằng:
b) Chứng minh AC2 = CH.BC
C4. Cho hình bình hành ABCD, trên cạnh AB lấy một điểm M. Đường thẳng DM cắt cạnh CB kéo dài tại N.
a) Chứng minh : MAD MBN
b) Chứng minh : MA.MN = MD.MB
Cho tam giác ABC nhọn. Các đường cao BD, CE cắt nhau tại H.a) Chứng minh 4 điểm B , D , H , E cùng thuộc một đường tròn.
Sửa đề: B,D,C,E
BD\(\perp\)AC
=>\(\widehat{BDC}=\widehat{ADB}=90^0\)
CE\(\perp\)AB
=>\(\widehat{AEC}=\widehat{BEC}=90^0\)
Xét tứ giác BEDC có
\(\widehat{BEC}=\widehat{BDC}=90^0\)
Do đó: BEDC là tứ giác nội tiếp
=>B,E,D,C cùng thuộc một đường tròn
cho tam giác ABC nhọn , các đường cao BD và CE cắt nhau tại H . Đường vuông góc AB tại B và đường vuông góc với AC tại C cắt nhau tại K . Gọi M là trung điểm của BC . Chứng minh
a , Chứng minh ADB∼ΔAEC và ΔAED ~ΔACB
d, AH cắt BC tại O . Chứng minh : BE . BA + CD . CA = BC2
g, cho góc ACB = 45o , gọi P là trung điểm của DC . Từ D kẻ đường thẳng vuông góc với BP tại I và cắt CK tại N . Tìm tỉ số diện tích của tứ giác CPIN và diện tích tam giác DCN
h, tam giác ABC có điềm kiện gì thì tứ giác BHCK là hình thoi ? Hình chữ nhật ?
Cho tam giác ABC nhọn ; có 2 đường cao BD và CE cắt nhau tại H.
a. Chứng minh rằng 4 điểm A , D , H , E thuộc 1 đường tròn.
b. Chứng minh 4 điểm B , C , E , D thuộc 1 đường tròn.
a: Xét tứ giác AEHD có
\(\widehat{AEH}+\widehat{ADH}=180^0\)
nên AEHD là tứ giác nội tiếp
hay A,E,H,D cùng thuộc 1 đường tròn
b: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}\)
nên BEDC là tứ giác nội tiếp
hay B,E,D,C cùng thuộc 1 đường tròn
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Hai đường cao BD và CE của tam giác ABC cắt nhau tại H. Tia BD và tia CE cắt đường tròn (O) lần lượt tại M, N (M khác B, N khác C)a) Chứng minh bốn điểm B, C, D, E cùng nằm trên một đường tròn.b) Chứng minh DE // MNc) Đường tròn đường kính AH cắt đường tròn (O) tại điểm thứ hai là K (K khác A). Tia KH cắt đường tròn (O) tại điểm thứ hai là Q. Tứ giác BHCQ là hình gì? Tại sao?d) Gọi giao điểm của HQ và BC là I. Chứng minh OI/MN > 1/4
a) Gọi G là trung điểm của BC
Ta có: ΔDBC vuông tại D(BD\(\perp\)AC tại D)
mà DG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(DG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(1)
Ta có: ΔEBC vuông tại E(CE\(\perp\)AB)
mà EG là đường trung tuyến ứng với cạnh huyền BC(G là trung điểm của BC)
nên \(EG=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)(2)
Ta có: G là trung điểm của BC(gt)
nên \(BG=CG=\dfrac{BC}{2}\)(3)
Từ (1), (2) và (3) suy ra GB=GC=GE=GD
hay B,C,D,E cùng nằm trên một đường tròn(đpcm)
Cho tam giác ABC nhọn, đường cao BD và CE cắt nhau tại H. Chứng minh rằng:
b) Tứ giác BEDC nội tiếp
b) Xét tứ giác BDEC có:
∠(BEC) = ∠(BDC) = 90 0
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BDEC là tứ giác nội tiếp
Cho tam giác ABC nhọn và các đường cao BD, CE, AM cắt nhau tại H
a) Chứng minh EH.EC=EA.EB
b) Chứng minh H là giao điểm bao đường phân giác của tam giác EDM
Cho tam giác ABC nhọn, kẻ 2 đường cao BD và CE cắt nhau tại H. a) Chứng minh tứ giác ADHE nội tiếp. b) CM tứ giác BEDC nội tiếp . c) góc acd = góc aed . d) góc edb =ecb
a) Xét tứ giác ADHE:
\(\widehat{AEH}+\widehat{ADH}=90^o+90^o=180^o.\)
Mà 2 góc này ở vị trí đối nhau.
\(\Rightarrow\) Tứ giác ADHE nội tiếp (dhnb).
b) Xét tứ giác BEDC:
\(\widehat{BEC}=\widehat{BDC}\left(=90^o\right).\)
Mà 2 đỉnh E; D kề nhau, cùng nhìn cạnh BC.
\(\Rightarrow\) Tứ giác BEDC nội tiếp (dhnb).
c) Sửa đề: Góc ACD \(\rightarrow\) Góc ACB.
Tứ giác BEDC nội tiếp (cmt).
\(\Rightarrow\widehat{AED}=\widehat{ACD}.\)
d) Tứ giác BEDC nội tiếp (cmt).
\(\Rightarrow\widehat{EDB}=\widehat{ECB}.\)
Cho tam giác ABC nhọn, đường cao BD và CE cắt nhau tại H. Chứng minh: P, H. BD + CH. CE = BC2.