\(a,ĐK:x,y\ne2\)

Đặt \(\left\{{}\begin{matrix}x-2=a\\y-2=b\end{matrix}\right.\)

\(HPT\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{a}+\dfrac{3}{b}=5\\\dfrac{3}{a}+\dfrac{2}{b}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{6}{a}+\dfrac{9}{b}=15\\\dfrac{6}{a}+\dfrac{4}{b}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{a}+\dfrac{3}{b}=5\\\dfrac{5}{b}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{a}+3=5\\b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=1\end{matrix}\right.\Leftrightarrow x=y=3\left(tm\right)\)

\(b,ĐK:x\ge3;y\ge1\)

Sửa: \(\sqrt{x-3}-\sqrt{y-1}=4\)

Đặt \(\left\{{}\begin{matrix}a=\sqrt{x-3}\ge0\\b=\sqrt{y-1}\ge0\end{matrix}\right.\)

\(HPT\Leftrightarrow\left\{{}\begin{matrix}a-2b=2\\a-b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-b=4\\-b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=6\\b=2\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x-3=36\\y-1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=39\\y=5\end{matrix}\right.\)

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để đề bài được rõ ràng hơn.

Đặt \(\dfrac{x}{\sqrt{4x-1}}=a\)

Theo đề, ta có phương trình:

a+1/a=2

\(\Leftrightarrow a+\dfrac{1}{a}=2\)

\(\Leftrightarrow\dfrac{a^2+1-2a}{a}=0\)

=>a=1

=>\(x=\sqrt{4x-1}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2=4x-1\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-2\right)^2=3\\x>=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow x\in\left\{2+\sqrt{3};2-\sqrt{3}\right\}\)

Đặt m = x - 1 .Điều kiện : m ≥ 0, x  ≥  1

Ta có : x -  x - 1 -3 = 0 ⇔ (x -1) - x - 1  -2 =0

⇔  m 2  -m - 2 =0

Phương trình  m 2  -m - 2 = 0 có hệ số a = 1, b = -1 , c = -2 nên có dạng

a – b + c = 0

Suy ra :  m 1  = -1 (loại) ,  m 2  = -(-2)/1 = 2

Với m =2 ta có: x - 1  =2 ⇒ x -1 =4 ⇔ x =5

Giá trị của x thỏa mãn điều kiện bài toán

Vậy phương trình đã cho có 1 nghiệm : x=5

a: =>(x^2-2x+1-1)^2+2(x-1)^2=1

=>(x-1)^4-2(x-1)^2+1+2(x-1)^2=1

=>(x-1)^4=0

=>x-1=0

=>x=1

b: =>(x^2+2)^2+3x(x^2+2)+2x^2-20x^2=0

=>(x^2+2)^2+3x(x^2+2)-18x^2=0

=>(x^2+2+6x)(x^2-3x+2)=0

=>\(x\in\left\{-3\pm\sqrt{7};1;2\right\}\)

\(\Leftrightarrow4\left|x-2\right|=\left(x-2\right)^2+4\)

Đặt \(\left|x-2\right|=t\ge0\)

\(\Rightarrow4t=t^2+4\Rightarrow t^2-4t+4=0\)

\(\Rightarrow\left(t-2\right)^2=0\Rightarrow t=2\)

\(\Rightarrow\left|x-2\right|=2\Rightarrow\left[{}\begin{matrix}x-2=2\\x-2=-2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=4\\x=0\end{matrix}\right.\)

Đặt m = 2 x 2  +x -2

Ta có: 2 x 2 + x - 2 2 +10 x 2  +5x -16 =0

⇔  2 x 2 + x - 2 2 +5(2 x 2  +x -2) -6 =0

⇔  m 2  +5m -6 =0

Phương trình  m 2  +5m -6 = 0 có hệ số a = 1, b = 5, c = -6 nên có dạng

a + b + c = 0

Suy ra :  m 1  =1 , m 2  =-6

m1 =1 ta có: 2 x 2  +x -2 =1 ⇔ 2 x 2  +x -3=0

Phương trình 2 x 2  +x -3 = 0 có hệ số a = 2, b = 1 , c = -3 nên có dạng

a +b+c=0

Suy ra:  x 1  =1 , x 2  =-3/2

Với m=-6 ta có: 2 x 2  +x -2 = -6 ⇔ 2 x 2  +x +4 =0

∆  =  1 2  -4.2.4 = 1 -32 = -31 < 0 . Phương trình vô nghiệm

Vậy phương trình đã cho có 2 nghiệm :  x 1  =1 , x 2  =-32

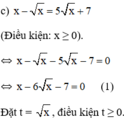
Khi đó (1) trở thành: t2 – 6t – 7 = 0 (2)

Giải (2): Có a = 1; b = -6; c = -7

⇒ a – b + c = 0

⇒ (2) có nghiệm t1 = -1; t2 = -c/a = 7.

Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.

+ Với t = 7 ⇒ √x = 7 ⇔ x = 49 (thỏa mãn).

Vậy phương trình đã cho có nghiệm x = 49.

1a) \(\left\{{}\begin{matrix}\left(x-3\right)\left(2y+5\right)=\left(2x+7\right)\left(y-1\right)\\\left(4x+1\right)\left(3y-6\right)=\left(6x-1\right)\left(2y+3\right)\end{matrix}\right.\)

<=> \(\left\{{}\begin{matrix}2xy+5x-6y-15=2xy-2x+7y-7\\12xy-24x+3y-6=12xy+18x-2y-3\end{matrix}\right.\)

<=> \(\left\{{}\begin{matrix}7x-13y=8\\-42x+5y=3\end{matrix}\right.\)( đến đây đơn giản rồi :)) )

Vậy ...

b) đặt a= 1/x và b = 1/y ( x,y khác 0)

ta có:

15a - 7b =9

4a + 9b = 35 

=> a= 2, b = 3

thay vào ta có:

2 = 1/x => x = 1/2

3 = 1/y => y = 1/3

b) ĐKXĐ : x,y khác 0

Đặt 1/x = a ; 1/y = b ( a,b khác 0 )

hpt đã cho trở thành \(\left\{{}\begin{matrix}15a-7b=9\\4a+9b=35\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)(tm)

=> \(\left\{{}\begin{matrix}\dfrac{1}{x}=2\\\dfrac{1}{y}=3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)(tm)

Vậy ...