Tập xác định của hàm số y = f ( x ) = x - 3 - 4 - x là:
A. [3; 4]
B. R \ (3; 4)
C. (3; 4)
D. R \ [3; 4].
Cho các hàm số y = f(x) xác định bởi: f(-3) = -2; f(-1) = -6; f(1,5) = 4; f(2) = 3; f(4) = 1,5
a) Cho biết tập xác định D của hàm số này.
b) Hàm số y = f(x) có thể được cho bởi công thức nào ?
Cho hàm số y = f(x) xác định trên tập số thực và có đạo hàm f'(x). Đồ thị hàm số y = f'(x) được cho bởi hình bên dưới. Biết rằng f(0) + f(1) - 2f(2) = f(4). - f(3). Giá trị nhỏ nhất của hàm số y = f(x) trên đoạn [0;4] là
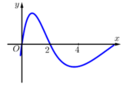
A. f(1)
B. f(0)
C. f(2)
D. f(4)
Chọn D
Từ đồ thị của hàm số y = f'(x) ta suy ra bảng biến thiên của hàm số y = f(x) trên đoạn như sau:
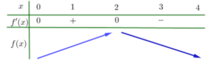
Từ bảng biến thiên, ta có nhận xét sau: ![]()
![]()
Ta lại có: f(0) + f(1) - 2f(2) = f(4). - f(3)
![]()
![]()
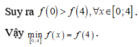
Cho hàm số y=f(x) xác định bởi công thức: \(y=\frac{-18}{\left|2x-1\right|}\)
a) Tìm đk xác định và tập xác định của hàm số.
b) Biết \(x\in\left\{-4;-2;-1;0;1;2;3\right\}\). Hãy viết tập hợp các cặp số xác định bởi hàm số y=f(x)
Câu a mình làm đc r, nhờ m.n làm hộ mình câu b và ý nhỏ này nx nhé, cũng nằm trong bài.
c) Tìm \(x\in Z\) để hàm số y=f(x) đạt GTNN? Tính giá trị đó.
Hàm số y = f(x) được xác định bởi tập hợp: {(-3 ; 6); (-2 ; 4); (0 ; 0); (1 ; -2); (3 ; -6)
Lập bảng các giá trị tương ứng x và y của các hàm số trên.
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Cho các mệnh đề sau đây:
(1) Hàm số f ( x ) = log 2 2 x - log 2 x 4 + 4 có tập xác định D = [ 0 ; + ∞ )
(2) Hàm số y = log a x có tiệm cận ngang
(3) Hàm số y = log a x ; 0 < a < 1 và Hàm số y = log a x , a > 1 đều đơn điệu trên tập xác định của nó
(4) Bất phương trình: log 1 2 5 - 2 x 2 - 1 ≤ 0 có 1 nghiệm nguyên thỏa mãn.
(5) Đạo hàm của hàm số y = ln 1 - cos x là sin x 1 - cos x 2
Hỏi có bao nhiêu mệnh đề đúng:
A. 0
B. 2
C. 3
D.1
tìm tập xác định của hàm số y=f(x) = \(\sqrt{3-x}+\sqrt{7x^2-x-6}\)
ĐKXĐ: \(\left\{{}\begin{matrix}3-x\ge0\\7x^2-x-6\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le3\\\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{6}{7}\end{matrix}\right.\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\le-\dfrac{6}{7}\\1\le x\le3\end{matrix}\right.\)
c1 tập xác định của hàm số \(y=\dfrac{sin2x+cosx}{tanx-sinx}\)
c2 tập xác định của hàm số \(y=\sqrt{1+cot^22x}\)
c3 tập xác định của hàm số \(y=cot\left(x-\dfrac{\pi}{4}\right)+tan\left(x-\dfrac{\pi}{4}\right)\)
1.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx}{cosx}-sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
2.
ĐKXĐ: \(sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
3.
ĐKXĐ: \(\left\{{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)\ne0\\cos\left(x-\dfrac{\pi}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{2}\right)\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
câu 2 ..... \(\dfrac{cos^22x}{sin^22x}=cot^22x\) nên suy ra sin2x khác 0 đúng hơm
còn câu 3, tui ko hiểu chỗ sin(2x-pi/4).. sao ở đây rớt xuống dợ
Hàm số y = f(x) được xác định bởi tập hợp:
|(-3 ; 6) ; (-2 ; 4) ; (0 ; 0) ; (1 ; -2) ; (3 ; -6)|
Lập bảng các giá trị tương ứng của x và y của hàm số trên