Đỉnh của parabol (P): y 3x2 – 2x + 1 là: A. 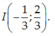B. 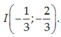C. 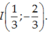D.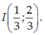
Đọc tiếp
Đỉnh của parabol (P): y = 3x2 – 2x + 1 là:
A. 
B. 
C. 
D. 
PB
Những câu hỏi liên quan
Cho parabol (P)
y
3
x
2
-
2
x
+
1
Điểm nào sau đây là đỉnh của (P)? A. I(0;1) B.
I
1
2
;
2
3
C.
I
-
1...
Đọc tiếp
Cho parabol (P) y = 3 x 2 - 2 x + 1 Điểm nào sau đây là đỉnh của (P)?
A. I(0;1)
B. I 1 2 ; 2 3
C. I - 1 3 ; 2 3
D. I 1 3 ; - 2 3
Câu 94. Cho hàm số y =x2 đồng biến trên khoảng
A.R B.(0,+∞) C.R\{0} D.(-∞,0)
Câu 95. Đỉnh của parabol y=-x2 +2x+3 có tọa độ là bao nhiêu.
Câu 96. Hàm số y=-x2 +2x+3 đồng biến trên khoảng:
A.(-1,+∞)
B.(-∞,-1)
C.(1,+∞)
D.(-∞,1)
Câu 94: B
Câu 95: \(A=\left(-\dfrac{b}{2a};-\dfrac{b^2-4ac}{4a}\right)\)
\(\Leftrightarrow A\left(\dfrac{-2}{2\cdot\left(-1\right)};\dfrac{-\left(2^2-4\cdot\left(-1\right)\cdot3\right)}{4\cdot\left(-1\right)}\right)\)
\(\Leftrightarrow A\left(1;4\right)\)
Đúng 1
Bình luận (1)
Đỉnh của parabol (P): y 3
x
2
- 2x + 1 là: A.
I
(
−
1
3
;
2
3
)
B.
I
(
−
1
3
;
−
2
3
)
C.
I
(
1
3
;
−
2
3...
Đọc tiếp
Đỉnh của parabol (P): y= 3 x 2 - 2x + 1 là:
A. I ( − 1 3 ; 2 3 )
B. I ( − 1 3 ; − 2 3 )
C. I ( 1 3 ; − 2 3 )
D. I ( 1 3 ; 2 3 )
Gọi A và B là 2 giao điểm của parabol (P):y=1/2x^2 và đường thẳng (d):y=1/2x-3. Hãy viết pt đường thẳng (d') tiếp xúcvới parabol (P) tại C sao cho tam giác ABC có diện tích lớn nhất
Bài 16 : xác định Parabol ( P ) : \(y=ax^2+bx+1\) , biết ( P) đi qua điểm A ( -2 , 1 ) và đỉnh nằm trên đường thẳng d : y +2x = 0
cho (P): y =2x +bx +c. Tìm các số b,c để đồ thị là một parabol thỏa:
a) Đỉnh A(-1;-2)
b) Đi qua hai điểm M(0;-1) và N(4;0).
c) Đi qua M(1;-2) và có hoành độ đỉnh là 2.
đ) Đi qua A(0;4) và có trục đối xứng là đường thẳng x = 1.
TN
13 tháng 2 2023 lúc 21:26
Cho parabol -3x2 cắt đường thẳng y=x-2 tại hai điểm P(x1;y1),Q(x2;y2).Giá trị của biểu thức x1x2+\(\dfrac{1}{2}\)y1y2 là
A.\(\dfrac{4}{3}\) B.\(\dfrac{8}{3}\) C.0 D.\(\dfrac{-4}{3}\)
Cho (P) : y= x^2 + bx+ c. Tìm các số b,c để đồ thị là một parabol thỏa:
a) Đỉnh A(1;2)
b) Đỉnh I(-3;1)
c) Đi qua điểm M(1;-1) và có hoành độ đỉnh bằng 4.
d) Đi qua M(1;2) và có hoành độ đỉnh là 2.
e) Đi qua A(3;3) và có trục đối xứng là đường thẳng x = 1.
Xác định trục đối xứng, tọa độ đỉnh , các giao điểm với trục tung và trục hoành của các parabol :
a, y= 2x2-x-2
b,y= -3x2-6x+4
c, y=-2x2-x+2
a: Trục đối xứng là x=-(-1)/4=1/4
Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot2\cdot\left(-2\right)}{4\cdot2}=-\dfrac{17}{8}\end{matrix}\right.\)
Thay y=0 vào (P), ta được:
2x^2-x-2=0
=>\(x=\dfrac{1\pm\sqrt{17}}{4}\)
thay x=0 vào (P), ta được:
y=2*0^2-0-2=-2
b: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-\left(-6\right)}{2\cdot\left(-3\right)}=\dfrac{6}{-6}=-1\\y=-\dfrac{\left(-6\right)^2-4\cdot\left(-3\right)\cdot4}{4\cdot\left(-3\right)}=7\end{matrix}\right.\)
=>Trục đối xứng là x=-1
Thay y=0 vào (P), ta được:
-3x^2-6x+4=0
=>3x^2+6x-4=0
=>\(x=\dfrac{-3\pm\sqrt{21}}{3}\)
Thay x=0 vào (P), ta được:
y=-3*0^2-6*0+4=4
c: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-\left(-1\right)}{2\cdot\left(-2\right)}=\dfrac{1}{-4}=\dfrac{-1}{4}\\y=-\dfrac{\left(-1\right)^2-4\cdot\left(-2\right)\cdot2}{4\cdot\left(-2\right)}=\dfrac{17}{8}\end{matrix}\right.\)
=>Trục đối xứng là x=-1/4
Thay y=0 vào (P), ta được:
-2x^2-x+2=0
=>2x^2+x-2=0
=>\(x=\dfrac{-1\pm\sqrt{17}}{4}\)
Thay x=0 vào (P), ta được:
y=-2*0^2-0+2=2
Đúng 0
Bình luận (0)