Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HK ⊥ AB (K ∈ AB). Chứng minh rằng:
b) A B 2 A C 2 = H B H C
PB
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HK ⊥ AB (K ∈ AB). Chứng minh rằng:
c) Cho ∠B = 30 0 , AC = 6 cm. Tính các cạnh AB, BC, AH
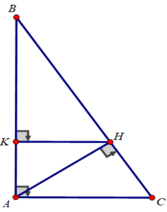
c) Xét tam giác ABC vuông tại A có ∠B = 30 0 , AC = 6 cm:
AB = AC.cotgB = 6.cotg 30 0 = 2 3 (cm)
AC = BC.sinB ⇒ 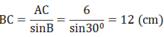
Tam giác ABC vuông tại A có AH là đường cao nên
AH.BC = AB.AC ⇒ 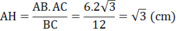
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Kẻ HK ⊥ AB (K ∈ AB). Chứng minh rằng:
a) AB. AK = HB. HC
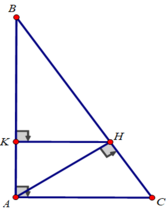
a) Xét tam giác ABC vuông tại A có đường cao AH
⇒ AH2 = HC.HB (1)
Xét tam giác AHB vuông tại H có đường cao HK
⇒ A H 2 = AK.AB (2)
Từ (1) và (2) ⇒ AK.AB = HC.HB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Từ B kẻ Bx vuông góc với AB, tia Bx cắt tia AH tại K .
a) Tứ giác ABKC là hình gì ? Tại sao ?
b) cho AB=a, góc B= 60 độ. chứng minh rằng: HC*HK=(a^2*√3)/4
a: Xét tứ giác ABKC có
AC//BK
góc BAC=90 độ
=>ABKC là hình thang vuông
b:
AH=AB*sin60=a*căn 3/2
BH=a/2
Xét ΔHAC vuông tại A và ΔHKB vuông tại H có
góc HAC=góc HKB
=>ΔHAC đồng dạng vớiΔHKB
=>HA/HK=HC/HB
=>HK*HC=HA*HB=a*căn 3/2*a/2=a^2*căn 3/4
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có góc B bằng 30 độ. Kẻ đường cao AH của tam giác ABC. Trên đoạn HB lấy K sao cho HC=HK.
a) Chứng minh tam giác AKC đều
b) Chứng minh K là trung điểm của BC
c) Qua K kẻ đường thẳng song song với AB cắt AH và AC theo thứ tự tại G và I. Chứng minh CG đi qua trung điểm của AK
a: Xét ΔAKC có
AH vừa là đường cao, vừa là trung tuyến
góc C=60 độ
=>ΔAKC đều
b: ΔKAB có góc KAB=góc KBA=30 độ
nên ΔKAB cân tạiK
=>KA=KB=KC
=>K là trung điểm của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , AB=3cm,AC= 4cm , đường cao AH .Kẻ HK vuông góc với AC tại K , kẻ HG vuông góc với AB tại G .
a, Chứng minh BH2= AB * BG
b, Chứng minh AC/HC=HB/AK
a, Xét tam giác ABH vuông tại H, đường cao HG
Ta có : \(NH^2=AB.BG\)( hệ thức lượng )
b, Xét tam giác AHC vuông tại H, đường cao HK
Ta có : \(AH^2=AK.AC\)( hệ thức lượng ) (1)
Xét tam giác ABC vuông tại A, đường cao AH
Ta có : \(AH^2=HB.HC\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra : \(AK.AC=HB.HC\Rightarrow\frac{AC}{HC}=\frac{HB}{AK}\)
giúp mk vs ạ cảm ơn
cảm ơn bn nhiều
Cho tam giác ABC vuông tại A, AB = 9cm, AC = 12cm, đường cao AH. Kẻ HK vuông góc với AC tại K, kẻ HG vuông góc với AB tại G.
a)Tính độ dài đoạn AH và các tỉ số lượng giác của góc B ; từ đó suy ra các tỉ số lượng giác của góc C.
b)Chứng minh rằng: AC/HC=HB/AK
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=92+122=225
BC=15cm
* AH.BC=AB.AC
AH.15=9.12
AH.15=108
AH=7,2cm
\(sinB=\dfrac{4}{5};cosB=\dfrac{3}{5};tanB=\dfrac{4}{3};cotanb=\dfrac{3}{4}\)
\(=>sinC=\dfrac{3}{5};cosC=\dfrac{4}{5};tanC=\dfrac{3}{4};cotanC=\dfrac{4}{3}\)
Đúng 1
Bình luận (0)
b)
tam giác ABC vuông tại A có
AC.AK=AH2
HB.HC=AH2
=>AC.AK=HB.HC
\(=>\dfrac{AC}{HC}=\dfrac{HB}{AK}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A (ABAC), đường cao AH (H thuộc BC). Qua C kẻ đường thẳng song song với AB cắt AH tại E. Kẻ HK vuông góc với AB tại K.1. Chứng minh: AB.EC – AH.EH HB.HC.2. Chứng minh: AK.HK.AH.BC HK2.HC2 + HB2.AK2.3. Đường thẳng qua A song song với BC cắt EC tại D, HD cắt AC tại I. vẽ 3 đường cao AM, HN, IP của tam giác AIH. Chứng minh: ba điểm C, M, K thẳng hàng.4. Chứng minh 3 điểm E, M, N thẳng hàng.5. Qua B kẻ đường thẳng song song với AC cắt HD tại S, BP cắ...
Đọc tiếp
Cho tam giác ABC vuông tại A (AB<AC), đường cao AH (H thuộc BC). Qua C kẻ đường thẳng song song với AB cắt AH tại E. Kẻ HK vuông góc với AB tại K.
1. Chứng minh: AB.EC – AH.EH = HB.HC.
2. Chứng minh: AK.HK.AH.BC = HK2.HC2 + HB2.AK2.
3. Đường thẳng qua A song song với BC cắt EC tại D, HD cắt AC tại I. vẽ 3 đường cao AM, HN, IP của tam giác AIH. Chứng minh: ba điểm C, M, K thẳng hàng.
4. Chứng minh 3 điểm E, M, N thẳng hàng.
5. Qua B kẻ đường thẳng song song với AC cắt HD tại S, BP cắt HK tại O. chứng minh 3 điểm A, O, S thẳng hàng.
Cho tam giác ABC và đường cao AH . Kẻ HI vuông góc với AB tại I, HK vuông góc với AC tại K
a) Chững minh tam giác ABC và tam giác AHB đồng dạng với nhau; AH^2=AI.AB
b) Chứng minh tam giác AIK đồng dạng với tam giác ACB
c) Đừng phân giác của góc AHB cắt AB tại E. Biết EB/AB=2/5. Chứng minh rằng BI/AI=4/9
cho tam giác abc vuông tại a(ab<ac), đường cao ah. kẻ hm vuông góc với ab tại m, hn vuông góc với ac tại n. i là trung điểm hc. k đối xứng với a qua i. câu a)cmr ac//hk, câu b)chứng minh rằng tứ giác mnck là hình thang cân, câu c) cho mn cắt ah tại o, co cắt ak tại d, chứng minh rằng ak=3ad
a/
Ta có
HI=CI (gt); AI=KI (gt) => ACKH là hbh (Tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AC//HK (Trong hbh 2 cạnh đối // với nhau)
b/
Ta có
\(HM\perp AB\left(gt\right);AC\perp AB\left(gt\right)\) => HM//AC
Mà HK//AC (cmt)
\(\Rightarrow HM\equiv HK\) (Từ 1 điểm ở ngoài 1 đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho) => M; K; H thẳng hàng
=> AC//MK => MNCK là hình thang
Ta có
AC//MK => AN//MH
\(AB\perp AC\left(gt\right);HN\perp AC\left(gt\right)\) => AB//HN => AM//HN
=> AMHN là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
\(\widehat{A}=90^o\)
=> AMHN là hình chữ nhật => AH=MN (trong HCN hai đường chéo bằng nhau)
Mà ACKH là hbh (cmt) => AH=CK (cạnh đối hbh)
=> MN=CK
=> hình thang MNCK có MN = CK => MNCK là hình thang cân
c/
Xét tg AHC có
OA=OH (Trong hình chữ nhật 2 đường chéo cắt nhau tại trung điểm mỗi đường)
HI=CI (gt)
=> D là trọng tâm của tg AHC \(\Rightarrow AD=\dfrac{2}{3}AI\)
Xét hình bình hành ACKH có
\(AI=KI\) (Trong hình bh 2 đường chéo cắt nhau tại trung điểm mỗi đường) \(\Rightarrow AI=\dfrac{1}{2}AK\)
\(\Rightarrow AD=\dfrac{2}{3}.\dfrac{1}{2}AK=\dfrac{1}{3}AK\Rightarrow AK=3AD\)
Đúng 0
Bình luận (0)





