b) Ta có: \(x^2-4x+20=0\)

\(\Leftrightarrow x^2-4x+4+16=0\)

\(\Leftrightarrow\left(x-2\right)^2+16=0\)(Vô lý)

Vậy: \(S=\varnothing\)

\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)

c) \(\left\{{}\begin{matrix}2\left(x-2\right)+3\left(1+y\right)=2\\3\left(x-2\right)-2\left(1+y\right)=-3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}6\left(x-2\right)+9\left(1+y\right)=6\\6\left(x-2\right)-4\left(1+y\right)=-6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}13\left(1+y\right)=12\\2\left(x-2\right)+3\left(1+y\right)=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{21}{13}\\y=-\dfrac{1}{13}\end{matrix}\right.\)

d) \(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-x-7y=-12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-x-7y=-12\\21x-7y=112\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}22x=124\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)

Bài toán này có hai cách giải:

Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.

Cách 2: Đặt ẩn phụ.

Cách 1:

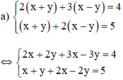
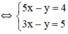 (hệ số của y bằng nhau nên ta trừ từng vế hai phương trình)

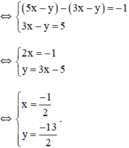
Vậy hệ phương trình có nghiệm duy nhất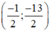 

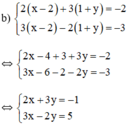
(Nhân hai vế pt 1 với 2; pt 2 với 3 để hệ số của y đối nhau)

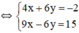 (Hệ số của y đối nhau nên ta cộng từng vế của hai pt)

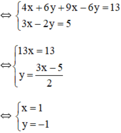
Vậy hệ phương trình có nghiệm duy nhất (1; -1).

Cách 2:

a) Đặt x + y = u và x – y = v (*)

Khi đó hệ phương trình trở thành

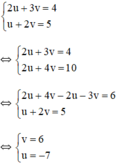
Thay u = -7 và v = 6 vào (*) ta được hệ phương trình:

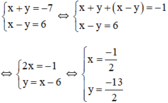
Vậy hệ phương trình có nghiệm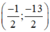 

b) Đặt x – 2 = u và y + 1 = v.

Khi đó hệ phương trình trở thành :

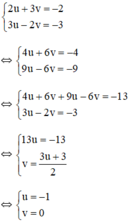
+ u = -1 ⇒ x – 2 = -1 ⇒ x = 1.

+ v = 0 ⇒ y + 1 = 0 ⇒ y = -1.

Vậy hệ phương trình có nghiệm (1; -1).

\(a,\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{2}{y}=2\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\left(x,y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{5}{y}=3\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{5}{3}\\\dfrac{2}{x}+\dfrac{9}{5}=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{8}\\y=-\dfrac{5}{3}\end{matrix}\right.\)

\(b,\Leftrightarrow\left\{{}\begin{matrix}\dfrac{60}{x}-\dfrac{28}{y}=36\\\dfrac{60}{x}-\dfrac{135}{y}=525\end{matrix}\right.\left(x,y\ne0\right)\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}+\dfrac{9}{y}=35\\-\dfrac{163}{y}=489\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{4}{x}-27=35\\y=-\dfrac{1}{3}\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{2}{31}\\y=-\dfrac{1}{3}\end{matrix}\right.\)

a: Ta có: \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=1\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}-\dfrac{2}{y}=2\\\dfrac{2}{x}-\dfrac{3}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=-3\\\dfrac{1}{x}-\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1}{3}\\\dfrac{1}{x}=1+\dfrac{1}{y}=1+\left(-3\right)=-2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{1}{3}\\x=\dfrac{-1}{2}\end{matrix}\right.\)

Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.

Cách 1:

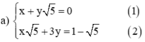
Từ (1) ta rút ra được x = -y√5 (*)

Thế (*) vào phương trình (2) ta được :

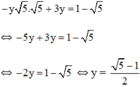
Thay y = 5 - 1 2 vào (*) ta được:  x = − 5 − 1 2 ⋅ 5 = 5 − 5 2

Vậy hệ phương trình có nghiệm  5 − 5 2 ; 5 − 1 2

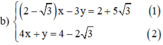
Từ (2) ta rút ra được y = -4x + 4 - 2 √3 (*)

Thế (*) vào phương trình (1) ta được:

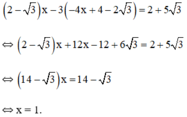
Thay x = 1 vào (*) ta được y = -4.1 + 4 - 2√3 = -2√3

Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)

Cách 2 :

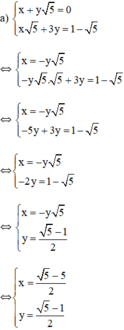
Vậy hệ phương trình có nghiệm duy nhất  5 − 5 2 ; 5 − 1 2

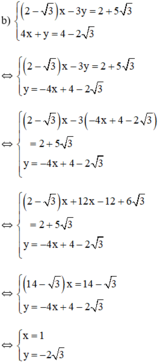
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)

Kiến thức áp dụng

Giải hệ phương trình 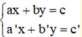 ta làm như sau:

Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).

Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .

Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.

a: Thay m=1 vào hệ phương trình, ta được:

\(\left\{{}\begin{matrix}x-y=1\\2x+y=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x=5\\x-y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{3}\\y=x-1=\dfrac{5}{3}-1=\dfrac{2}{3}\end{matrix}\right.\)

b: Để hệ có nghiệm duy nhất thì \(\dfrac{m}{2}\ne-\dfrac{1}{m}\)

=>\(m^2\ne-2\)(luôn đúng)

\(\left\{{}\begin{matrix}mx-y=1\\2x+my=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-1\\2x+m\left(mx-1\right)=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=mx-1\\x\left(m^2+2\right)=m+4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=\dfrac{m+4}{m^2+2}\\y=\dfrac{m\left(m+4\right)}{m^2+2}-1=\dfrac{m^2+4m-m^2-2}{m^2+2}=\dfrac{4m-2}{m^2+2}\end{matrix}\right.\)

x+y=2

=>\(\dfrac{m+4+4m-2}{m^2+2}=2\)

=>\(2m^2+4=5m+2\)

=>\(2m^2-5m+2=0\)

=>(2m-1)(m-2)=0

=>\(\left[{}\begin{matrix}2m-1=0\\m-2=0\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=2\end{matrix}\right.\)

e: \(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=1\\\dfrac{3}{x}+\dfrac{4}{y}=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}-\dfrac{3}{y}=3\\\dfrac{3}{x}+\dfrac{4}{y}=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-7}{y}=-2\\\dfrac{1}{x}-\dfrac{1}{y}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{7}{2}\\\dfrac{1}{x}=1+\dfrac{2}{7}=\dfrac{9}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{7}{2}\\x=\dfrac{7}{9}\end{matrix}\right.\)

Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.

ĐK: $m\neq 0$

a) Khi $m=2,$ hệ phương trình là:

\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)

b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)

c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:

\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)

d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)

Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$