Giải các hệ phương trình: 2 x - 3 2 y - 5 = 3 x + 1 3 y - 4 2 x - 3 - 3 y + 2 = - 16
PB
Những câu hỏi liên quan
bài 1: giải các phương trình sau :
a) x^3-5x=0 b) căn bậc 2 của x-1=3
bài 2 :
cho hệ phương trình : {2x+my;3x-y=0 (I)
a) giải hệ phương trình khi m=0
b) tìm giá trị của m để hệ (I) có nghiệm (x;y) thỏa mãn hệ thức :
x-y+m+1/m-2=-4
bài 3:giải các phương trình sau
a)5x-2/3=5x-3/2 b) 10x+3/12=1+6x+8/9 c) 2(x+3/5)=5-(13/5+x) d) 7/8x-5(x-9)=20x+1,5/6
cho hệ phương trình
\(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y+1\end{matrix}\right.\)
a)giải hệ phương trình khi m=2
b)giải hệ phương trình theo m
c)tìm m để hệ có nghiệm (x;y) là các số dương
d)tìm m để hệ phương trình có nghiệm thỏa mãn x^2+y^2=1
Mình mạn phép sửa lại phương trình $2$ của bạn là $mx+3y=1$ nhé.
ĐK: $m\neq 0$
a) Khi $m=2,$ hệ phương trình là:
\(\left\{{}\begin{matrix}-4x+y=5\\2x+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+y=5\\4x+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-1\)
b) \(\left\{{}\begin{matrix}-2mx+y=5\\mx+3y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2mx+y=5\\2mx+6y=2\end{matrix}\right.\Rightarrow7y=7\Leftrightarrow y=1\Rightarrow x=-\dfrac{2}{m}\)
c) Do ta luôn có $y=1$ là số dương nên chỉ cần chọn $m$ sao cho:
\(x=-\dfrac{2}{m}>0\Leftrightarrow m< 0\)
d) \(x^2+y^2=1\Leftrightarrow\left(-\dfrac{2}{m}\right)^2+1^2=1\Leftrightarrow\dfrac{4}{m^2}=0\) (vô lý)
Vậy không tồn tại $m$ sao cho $x^2+y^2=1.$
Đúng 3
Bình luận (0)
Cho phương trình: x2 - 2 (m - 1)x - m - 3 = 0 (1)
1) Giải phương trình với m = -3
2) Tìm m để phương trình (1) có 2 nghiệm thoả mãn hệ thức \(x_1^2+x_2^2\) = 10.
3) Tìm hệ thức liên hệ giữa các nghiệm không phụ thuộc giá trị của m
1, bạn tự giải
2,
\(\Delta'=\left(m-1\right)^2-\left(-m-3\right)=m^2-2m+1+m+3=m^2-m+4=\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}>0\)
Vậy pt luôn có 2 nghiệm x1 ; x2 khi \(\left(m-\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ne0\left(luondung\right)\)
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=-m-3\end{matrix}\right.\)
Ta có \(\left(x_1+x_2\right)^2-2x_1x_2=10\)
Thay vào ta được \(4\left(m-1\right)^2-2\left(-m-3\right)=10\)
\(\Leftrightarrow4m^2-8m+4+2m+6=10\Leftrightarrow4m^2-6m=0\)
\(\Leftrightarrow m\left(4m-6\right)=0\Leftrightarrow m=0;m=\dfrac{3}{2}\)
Đúng 0
Bình luận (0)
cho hệ phương trình:{mx-y=1 và x+my=2
1,giải hệ phương trình theo tham số m
2,gọi nghiệm của hệ phương trình là(x,y). Tìm các giá trị m để x+y=1
3, tìm đẳng thức liên hệ giưa x và y không phụ thuộc vào m
Giải các phương trình và hệ phương trình sau:
1) \(\dfrac{x-1}{3}=x+1\)
2) \(\sqrt{16x^2+8x+1}-2=x\)
3)\(\left\{{}\begin{matrix}2x+y=17\\x-2y=1\end{matrix}\right.\)
\(1,\dfrac{x-1}{3}=x+1\\ \Leftrightarrow x-1=3x+3\\ \Leftrightarrow3x-x=3+1\\ \Leftrightarrow x=2\)
PT có tập nghiệm S = {2}
\(2,\sqrt{16x^2+8x+1}-2=x\\ \Leftrightarrow\sqrt{\left(4x+1\right)^2}-2=x\\\Leftrightarrow 4x+1-2=x\\ \Leftrightarrow4x-x=2-1\\ \Leftrightarrow x=\dfrac{1}{3}\)
PT có tập nghiệm S = {1/3}
\(3,\left\{{}\begin{matrix}2x+y=17\\x-2y=1\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=17\\2x-4y=2\end{matrix}\right.\\ \Leftrightarrow\left(2x+y\right)-\left(2x-4y\right)=17-2\\ \Leftrightarrow5y=15\\ \Leftrightarrow y=3\\ \Leftrightarrow2x+3=17\\ \Leftrightarrow2x=14\\ \Leftrightarrow x=7\)
PTHH có tập nghiệm (x; y) là (7; 3)
Đúng 1
Bình luận (0)
Giải các phương trình và hệ phương trình sau:1. Phương trình bậc hai và hệ thức vi éta. -3² + 2x + 80b. 5x² - 6x - 10c. -3x² + 14x - 802. Nhẩm nghiệm của các phương trình bậc hai sau:a) 5x² + 3x -20b) -18x² + 7x +110c) x² + 1001x + 1000 0d) -7x² - 8x + 150e) 2x³ - 4x² - 6x 03. Tìm hai số biết tổng và tích của chúng:a) u + v 14, uv40b) u + v -7, uv12c) u + v -5, uv -24
Đọc tiếp
Giải các phương trình và hệ phương trình sau:
1. Phương trình bậc hai và hệ thức vi ét
a. -3² + 2x + 8=0
b. 5x² - 6x - 1=0
c. -3x² + 14x - 8=0
2. Nhẩm nghiệm của các phương trình bậc hai sau:
a) 5x² + 3x -2=0
b) -18x² + 7x +11=0
c) x² + 1001x + 1000 =0
d) -7x² - 8x + 15=0
e) 2x³ - 4x² - 6x =0
3. Tìm hai số biết tổng và tích của chúng:
a) u + v =14, uv=40
b) u + v = -7, uv=12
c) u + v = -5, uv = -24
3:
a: u+v=14 và uv=40
=>u,v là nghiệm của pt là x^2-14x+40=0
=>x=4 hoặc x=10
=>(u,v)=(4;10) hoặc (u,v)=(10;4)
b: u+v=-7 và uv=12
=>u,v là các nghiệm của pt:
x^2+7x+12=0
=>x=-3 hoặc x=-4
=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)
c; u+v=-5 và uv=-24
=>u,v là các nghiệm của phương trình:
x^2+5x-24=0
=>x=-8 hoặc x=3
=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)
Đúng 0
Bình luận (0)
Giải các hệ phương trình sau:
{ (x - 5)(y - 2) = (x + 2)(y - 1)
{ (x - 4)(y + 7) = (x - 3)(y + 4)
\(\left\{{}\begin{matrix}\left(x-5\right)\left(y-2\right)=\left(x+2\right)\left(y-1\right)\\\left(x-4\right)\left(y+7\right)=\left(x-3\right)\left(y+4\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}xy-2x-5y+10=xy-x+2y-2\\xy+7x-4y-28=xy+4x-3y-12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+7y=12\\3x-y=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x+21y=36\\3x-y=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}22y=20\\x+7y=12\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{62}{11}\\y=\dfrac{10}{11}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Giải các hệ phương trình sau bằng phương pháp thế:
a
)
x
+
y
5
0
x
5
+...
Đọc tiếp
Giải các hệ phương trình sau bằng phương pháp thế:
a ) x + y 5 = 0 x 5 + 3 y = 1 − 5 b ) ( 2 − 3 ) x − 3 y = 2 + 5 3 4 x + y = 4 − 2 3
Bài toán giải hệ phương trình bằng phương pháp thế có 2 cách trình bày.
Cách 1:
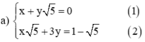
Từ (1) ta rút ra được x = -y√5 (*)
Thế (*) vào phương trình (2) ta được :
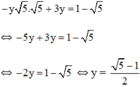
Thay y = 5 - 1 2 vào (*) ta được: x = − 5 − 1 2 ⋅ 5 = 5 − 5 2
Vậy hệ phương trình có nghiệm 5 − 5 2 ; 5 − 1 2
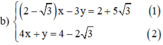
Từ (2) ta rút ra được y = -4x + 4 - 2 √3 (*)
Thế (*) vào phương trình (1) ta được:
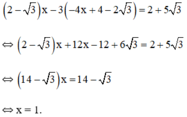
Thay x = 1 vào (*) ta được y = -4.1 + 4 - 2√3 = -2√3
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)
Cách 2 :
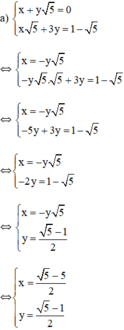
Vậy hệ phương trình có nghiệm duy nhất 5 − 5 2 ; 5 − 1 2
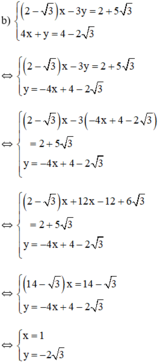
Vậy hệ phương trình có nghiệm duy nhất (1; -2√3)
Kiến thức áp dụng
Giải hệ phương trình 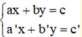 ta làm như sau:
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
Đúng 0
Bình luận (0)
Bài tập 1 Cho hệ phương trình (1)1. Giải hệ phương trình (1) khi m 3 .2. Tìm m để hệ phương trình có nghiệm x và y .3. Tìm nghiệm của hệ phương trình (1) theo m.
Đọc tiếp
Bài tập 1 Cho hệ phương trình  (1)
(1)
1. Giải hệ phương trình (1) khi m = 3 .
2. Tìm m để hệ phương trình có nghiệm x = ![]() và y =
và y = ![]() .
.
3. Tìm nghiệm của hệ phương trình (1) theo m.
1. Giải phương trình: \(\sqrt{x-2}+\sqrt{4-x}=\sqrt{2}\) .
2. Giải phương trình: \(4x^4-7x^3+9x^2-10x+4=0\).
3. Giải hệ phương trình: \(\left\{{}\begin{matrix}x^2+y^2=3-xy\\x^4+y^4=2\end{matrix}\right.\) .
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
Đúng 2
Bình luận (0)
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
Đúng 2
Bình luận (0)
Nãy mình tìm được một cách giải tương tự cho câu 2.
PT \(\Leftrightarrow\left(x-1\right)\left(4x^3-3x^2+6x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x^3-3x^2+6x-4=0\left(1\right)\end{matrix}\right.\)
Vậy pt có 1 nghiệm bằng 1.
\(\left(1\right)\Rightarrow8x^3-6x^2+12x-8=0\)
\(\Leftrightarrow7x^3+x^3-6x^2+12x-8=0\)
\(\Leftrightarrow\left(x-2\right)^3=-7x^3\)
\(\Leftrightarrow x-2=-\sqrt[3]{7}x\)
\(\Leftrightarrow x=\dfrac{2}{1+\sqrt[3]{7}}\)
Vậy pt có nghiệm \(S=\left\{1;\dfrac{2}{1+\sqrt[3]{7}}\right\}\)
Lưu ý: Nghiệm của người kia hoàn toàn tương đồng với nghiệm của mình (\(\dfrac{2}{1+\sqrt[3]{7}}=\dfrac{1}{4}\left(1-\sqrt[3]{7}+\sqrt[3]{49}\right)\))
Đúng 0
Bình luận (0)
Xem thêm câu trả lời






