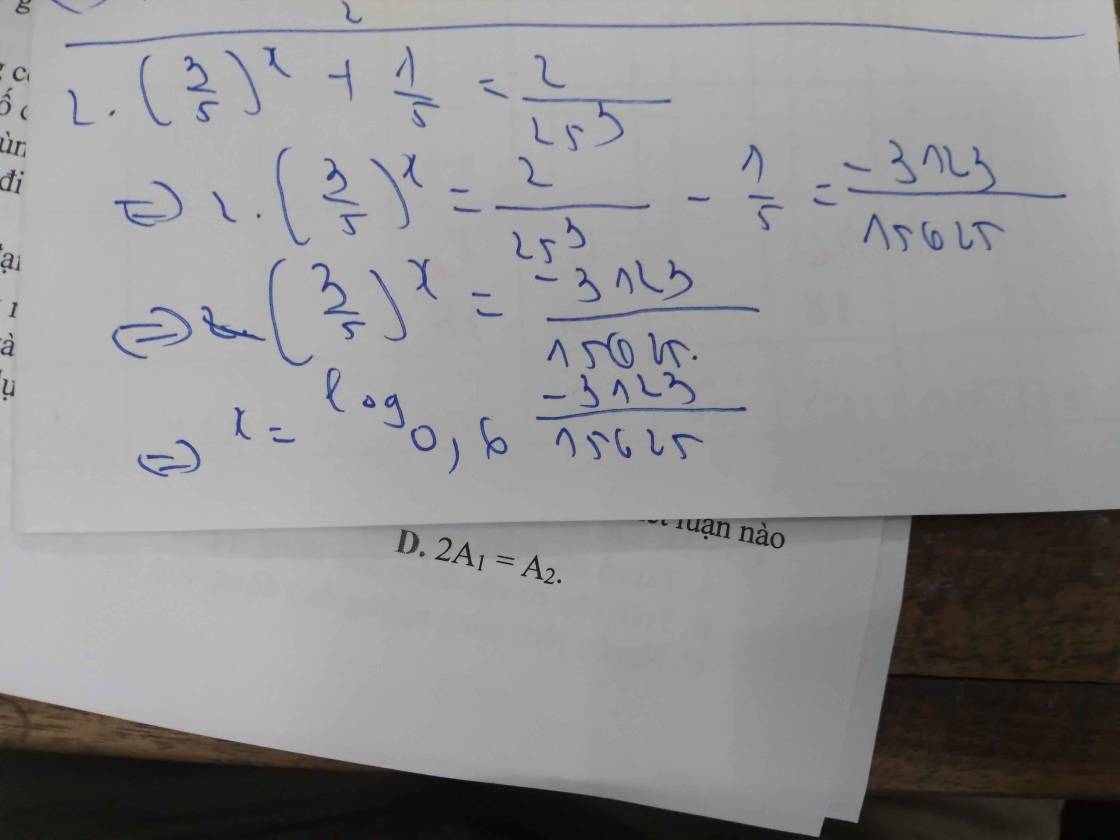\(B\left(x\right)=x^5+3x^3+x=x\left(x^4+3x^2+1\right)=x\left(x^4+x^2+x^2+1+x^2\right)=x\left[x^2\left(x^2+1\right)+x^2+1+x^2\right]\)

\(=x\left[\left(x^2+1\right)\left(x^2+1\right)+x^2\right]=x\left[\left(x^2+1\right)^2+x^2\right]\)

Vì: \(x^2+1>0,x^2\ge0\)nên \(\left(x^2+1\right)^2+x^2>0\)

Vậy B(x)  có nghiệm khi x=0

1: \(\dfrac{x-1}{3}=\dfrac{y-2}{4}=\dfrac{z+7}{5}\)

mà x+y-z=8

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x-1}{3}=\dfrac{y-2}{4}=\dfrac{z+7}{5}=\dfrac{x-1+y-2-z-7}{3+4-5}=\dfrac{8-3-7}{2}=\dfrac{-2}{2}=-1\)

=>\(\left\{{}\begin{matrix}x-1=-1\cdot3=-3\\y-2=-1\cdot4=-4\\z+7=-1\cdot5=-5\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-2\\y=-2\\z=-12\end{matrix}\right.\)

2: \(\dfrac{x+1}{3}=\dfrac{y+2}{-4}=\dfrac{z-3}{5}\)

mà 3x+2y=47-42=5

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x+1}{3}=\dfrac{y+2}{-4}=\dfrac{z-3}{5}=\dfrac{3x+3+2y+4}{3\cdot3+2\left(-4\right)}=\dfrac{5+7}{9-8}=12\)

=>\(\left\{{}\begin{matrix}x+1=12\cdot3=36\\y+2=-12\cdot4=-48\\z-3=12\cdot5=60\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=35\\y=-48-2=-50\\z=60+3=63\end{matrix}\right.\)

\(a,\Rightarrow4x\left(x^2-9\right)=0\\ \Rightarrow4x\left(x-3\right)\left(x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ b,\Rightarrow\left(3x-5-x-1\right)\left(3x-5+x+1\right)=0\\ \Rightarrow\left(2x-6\right)\left(4x-4\right)=0\\ \Rightarrow2\left(x-3\right)4\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

a) \(\Rightarrow4x\left(x^2-9\right)=0\)

\(\Rightarrow4x\left(x-3\right)\left(x+3\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)

b) \(\Rightarrow\left(3x-5-x-1\right)\left(3x-5+x+1\right)=0\)

\(\Rightarrow\left(2x-6\right)\left(4x-4\right)=0\)

\(\Rightarrow8\left(x-3\right)\left(x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=3\\x=1\end{matrix}\right.\)

\(\sqrt{4-x^2}=\sqrt{x+2}\) (ĐK: \(-2\le x\le2\))

\(\Leftrightarrow4-x^2=x+2\)

\(\Leftrightarrow x^2+x-2=0\)

\(\Leftrightarrow x^2+2x-x-2=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\)

_______

\(\sqrt{9x^2-4}=2\sqrt{3x-2}\) (ĐK: \(x\ge\dfrac{2}{3}\)) 

\(\Leftrightarrow9x^2-4=4\left(3x-2\right)\)

\(\Leftrightarrow9x^2-4=12x-8\)

\(\Leftrightarrow9x^2-12x+4=0\)

\(\Leftrightarrow\left(3x-2\right)^2=0\)

\(\Leftrightarrow3x=2\)

\(\Leftrightarrow x=\dfrac{2}{3}\left(tm\right)\)

a:Ta có: \(x\left(x-1\right)+x=4\)

\(\Leftrightarrow x^2-x+x=4\)

\(\Leftrightarrow x^2=4\)

hay \(x\in\left\{2;-2\right\}\)

b: Ta có: \(3x\left(x-5\right)-2x+10=0\)

\(\Leftrightarrow\left(x-5\right)\left(3x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\end{matrix}\right.\)

c: Ta có: \(5x^2-3x-2=0\)

\(\Leftrightarrow5x^2-5x+2x-2=0\)

\(\Leftrightarrow\left(x-1\right)\left(5x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{2}{5}\end{matrix}\right.\)

d: Ta có: \(x^4-11x^2+18=0\)

\(\Leftrightarrow x^4-9x^2-2x^2+18=0\)

\(\Leftrightarrow x^2\left(x^2-9\right)-2\left(x^2-9\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x+3\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\\x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)

a) x(x-1)+x=4

⇔x²=4⇔\(x=\pm2\)

b)3x(x-5)-2x+10=0

⇔3x(x-5)-2(x-5)=0

⇔(x-5)(3x-1)=0

\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{1}{3}\end{matrix}\right.\)

c)5x²-3x-2=0

⇔ 5x(x-1)+2(x-1)=0

⇔ (x-1)(5x+2)=0

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{2}{5}\end{matrix}\right.\)

d)x⁴-11x²+18=0

⇔ x²(x²-2)-9(x²-2)=0

⇔ (x²-2)(x²-9)=0

\(\Leftrightarrow\left[{}\begin{matrix}x^2=2\\x^2=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\pm\sqrt{2}\\x=\pm3\end{matrix}\right.\)

\(\frac{1}{x+2}+\frac{5}{x-2}=\frac{3x-12}{x^2-4}\)

ĐKXĐ \(x\ne\pm2\)

\(\frac{1}{x+2}+\frac{5}{x-2}=\frac{3x-12}{x^2-4}\)

\(\Leftrightarrow\frac{x-2+5\left(x+2\right)}{x^2-4}=\frac{3x-12}{x^2-4}\)

\(\Leftrightarrow x-2+5x+10=3x-12\)

\(\Leftrightarrow6x+8=3x-12\)

\(\Leftrightarrow3x=20\Leftrightarrow x=\frac{20}{3}\left(tm\right)\)