Xét sự biến thiên của hàm số y = 4 x + 5 + x − 1 trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình 4 x + 5 + x − 1 = 4 x 2 + 9 + x
A. 1 nghiệm duy nhất
B. 2 nghiệm
C. 3 nghiệm
D. Vô nghiệm
Xét sự biến thiên của hàm số y = 4 x + 5 + x − 1 trên tập xác định của nó. Áp dụng tìm số nghiệm của phương trình 4 x + 5 + x − 1 = 3
A. 1 nghiệm duy nhất
B. 2 nghiệm
C. 3 nghiệm
Vô nghiệm
xét sự biến thiên của hàm số sau trên tập xác định của nó và lập bảng biến thiên:
a, \(y=-x^2-2x+3\)
b, \(y=\dfrac{x+1}{x-2}\)
a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
Xét sự biến thiên của hàm số sau:
1, \(y=4-3x\)
2, \(y=x^2+4x-5\)
3, \(y=\dfrac{x}{x-1}trên\left(-\infty;1\right)\)
4, \(y=\dfrac{2}{x-2}trên\left(-\infty;2\right)vàtrên\left(2;+\infty\right)\)
Hi guys, please help me :))))
I need it now !!!!
1 nghịch biến(a<0)
2 đồng biến
3,4 thay các g trị tm đk vào
hojk tốt
Cho hàm số \(y=\sqrt{x-1}+x^2-2x\)
a, Xét sự biến thiên của hàm số đã cho trên [ 1;+\(\infty\))
b, Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn \(\left[2;5\right]\)
please help me
i need it now
Xét sự biến thiên của hàm số f(x) = x + 1 x trên khoảng (1;+ ∞ ). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng (1; + ∞ ).
B. Hàm số nghịch biến trên khoảng (1; + ∞ ).
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng (1; + ∞ ).
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng (1; + ∞ ).
Xét sự biến thiên của hàm số y = 3 x − 1 trên khoảng (1; + ∞ )
A. Đồng biến
B. Nghịch biến
C. Vừa đồng biến, vừa nghịch biến
D. Không đồng biến, cũng không nghịch biến
Xét sự biến thiên của hàm số sau trên các khoảng đã chỉ ra
a) y=2x+3 trên R
b) y=\(\frac{x}{x^2+1}\) trên (0;1)
Một học sinh khảo sát sự biến thiên của hàm số như sau:
I. Tập xác định: D = ℝ
II. Sự biến thiên: y ' = x 2 − x − 2 ; y ' = 0 ⇔ x = − 1 x = 2
lim x → − ∞ y = − ∞ ; lim x → + ∞ y = + ∞
III. Bảng biến thiên:
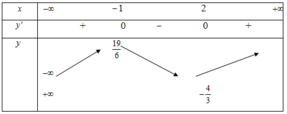
IV. Vậy hàm số đồng biến trên nghịch biến trên khoảng
−
∞
;
−
1
∪
2
;
+
∞
, nghịch biến trên khoảng
−
1
;
2
Lời giải trên sai từ bước nào?
A. Bước IV
B. Bước I
C. Bước II
D. Bước III
Đáp án là D.
• Sai ở bước III (bảng biến thiên)
Xét sự biến thiên của hàm số y=\(\frac{2}{3-x}\) trên khoảng (3;+ vô cực)
x>3
nên 3-x<0
=>Hàm số nghịch biến khi x>3