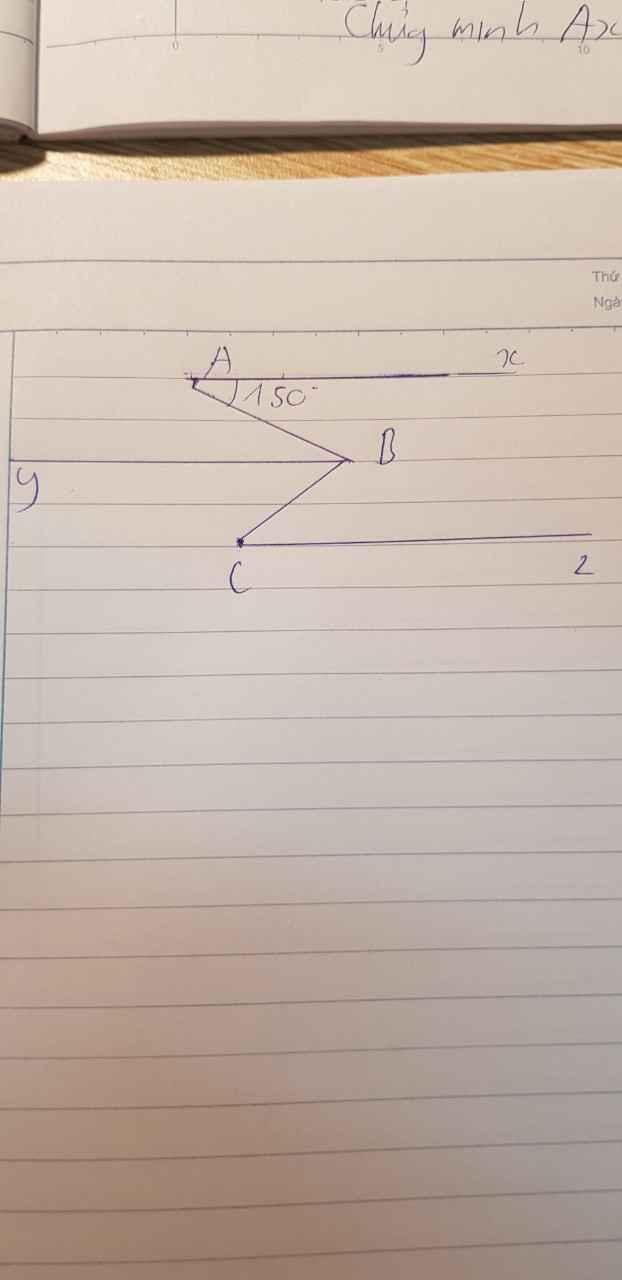
Cho hình vẽ bên. Chứng minh:
a) Ax // By
b) By // Cz
PB
Những câu hỏi liên quan
Trong hình vẽ bên, cho ABC ̂ 800, By là tia phân giác của ABC ̂.Chứng minh rằng:a) Ax ⫽ By theo hai cách b) Ax ⫽ Cz
Đọc tiếp
Trong hình vẽ bên, cho ABC ̂ = 800, By là tia phân giác của ABC ̂.
Chứng minh rằng:
a) Ax ⫽ By theo hai cách b) Ax ⫽ Cz
Bai 3:Cho hình vẽ dưới đây. Chứmg minh:a) Ax // Byb) By // Cz A B C y t x z 150 0 120 0 90 0 60 0
Đọc tiếp
Bai 3:Cho hình vẽ dưới đây. Chứmg minh:
a) Ax // By
b) By // Cz
\(a,\widehat{xAB}+\widehat{xAt}=180^0\left(kề.bù\right)\\ \Rightarrow\widehat{xAB}=180^0-60^0=120^0\\ \Rightarrow\widehat{xAB}=\widehat{yBA}\left(=120^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(Ax//By\)
\(b,\widehat{yBC}+\widehat{ABC}+\widehat{yBA}=360^0\\ \Rightarrow\widehat{yBC}=360^0-120^0-90^0=150^0\\ \Rightarrow\widehat{yBC}=\widehat{BCz}\left(=150^0\right)\)
Mà 2 góc này ở vị trí so le trong nên \(By//Cz\)
Đúng 2
Bình luận (0)
Cho hình vẽ bên. Chứng minh:
a) By // xx'
b) By // Cz
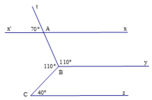
a) Ta có x'At ^ + tAx ^ = 180 ∘ (hai góc kề bù)
mà x'At ^ = 70 ∘
⇒ xAt ^ = 180 ∘ − 70 ∘ = 110 ∘
Mặt khác ABy ^ = 110 ∘
⇒ xAt ^ = ABy ^ mà hai góc này ở vị trí đồng vị
⇒ By // xx'
b)
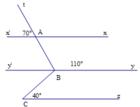
Kẻ tia By' là tia đối của tia By
Vì By // xx' nên By' // xx'
⇒ x'At ^ = ABy' ^ = 70 ∘ (hai góc đồng vị)
Mặt khác ABC ^ = ABy' ^ + y'BC ^
Mà ABC ^ = 110 ∘ và ABy' ^ = 70 ∘
⇒ y'BC ^ = 110 ∘ − 70 ∘ = 40 ∘
Ta lại có BCz ^ = 40 ∘
⇒ y'BC ^ = BCz ^ mà hai góc này ở vị trí so le trong
⇒ By // Cz
Đúng 0
Bình luận (0)
Cho hình vẽ biết Cz//Ax,góc c=30°,góc ACB=110° a)chứng minh Ax//By,Cz//By b)tính góc CBy c)tính số đo góc acd
Giúp tui với mn ơi cần gấp lắm ròi :<
Đúng 0
Bình luận (0)
Cho hình vẽ bên, biết
y
B
n
^
-
148
°
m
A
x
^
z
C
n
^
32
°
. Chứng minh ba đường thẳng Ax, By và Cz đôi một song song.
Đọc tiếp
Cho hình vẽ bên, biết y B n ^ - 148 ° = m A x ^ = z C n ^ = 32 ° . Chứng minh ba đường thẳng Ax, By và Cz đôi một song song.
ND
30 tháng 8 2023 lúc 9:03
Cho hình vẽ:
45* 135* 75* 30* A x B C y z
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
Đọc tiếp
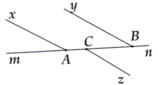
Cho hình vẽ:
a, Chứng tỏ rằng Ax // By b, Chứng minh By // Cz
a) Vẽ tia By' là tia đối của tia By
Ta có:
∠ABy' + ∠ABy = 180⁰ (kề bù)
⇒ ∠ABy' = 180⁰ - ∠ABy
= 180⁰ - 135⁰
= 45⁰
⇒ ∠ABy' = ∠BAx = 45⁰
Mà ∠ABy' và ∠BAx là hai góc so le trong
⇒ By // Ax
b) Ta có:
∠CBy' = ∠ABC - ∠ABy'
= 75⁰ - 45⁰
= 30⁰
⇒ ∠CBy' = ∠BCz = 30⁰
Mà ∠CBy' và ∠BCz là hai góc so le trong
⇒ By // Cz
Đúng 0
Bình luận (0)
Bài 13: Cho hình vẽ. Chứng minh: Ax//By//Cz.
Bài 14: Cho hình vẽ. Biết mAx=60 độ; mBy= 120 độ, BCz=150 độ.Chứng minh: Ax//By//Cz. Giúpp mình với ạ. Mình đang cần gấpp.
Helpp
*Kẻ By’ là tia đối của tia By => ABy kề bù với ABy’
=> ABy + ABy’ = 180
=> 120 + ABy’ = 180
=> ABy’ = 60
Ta có mAx = 60 =ABy’ , mà mAx và ABy’ ở vị trí đồng vị => Ax // By (1)
*Ta có yBC + CBA + ABy = 360
=> yBC + 90 + 120 = 360
=> yBC = 150
Ta có BCz = 150 = yBC, mà 2 góc này ở vị trí so le trong => By // Cz (2)
Từ (1), (2) => đpcm
Đúng 0
Bình luận (0)
Cho hình vẽ bên, biết: x A B ^ = 30 O , A B C ^ = 90 O , By //Cz //Ax. Tính số đo B C z ^ .
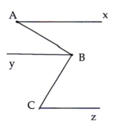
cho hình vẽ cho BAC=50 ABC=90 ABy=40 BCz=50 Chứng minh Ax//By By//Cz