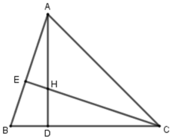
Xét tam giác ABD và CBE có:

E = D =  90 ∘  

Chung B

=> ΔABD ~ ΔCBE (g - g)

⇒ B A D ^ = B C E ^ = D C H ^ (góc t/ư)

Xét ΔADB và ΔCDH có:

A D B ^ = C D H ^ = 90 ∘

B A D ^ = D C H ^ (cmt)

=> ΔADB ~ ΔCDH (g - g)

Vậy A, B đều đúng

Đáp án: C

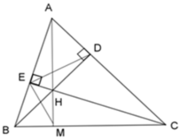
Theo cmt ta có: ΔHBE ~ ΔHCD

⇒ H E H D = H B H C ⇔ H E H B = H D H C

Xét ΔHED và ΔHBC ta có:

H E H B = H D H C (chứng minh trên)

E H D ^ = H A E ^ (hai góc đối đỉnh)

H D E ^ = H A E ^

=> ΔHED ~ ΔHBC (c - g - c)

⇒ H D E ^ = H C B ^ (1)

Mà đường cao BD và CE cắt nhau tại H (theo giả thiết)

=> H là trực tâm của ΔABC

=> AH  BC tại M => AMB = 90 ∘

Xét ΔAMB và ΔCEB có:

C E B ^ = A M B ^ = 90 ∘

B chung

=> ΔAMB ~ ΔCEB (g - g)

⇒ M A B ^ = E C B ^ hay H A E ^ = H C B ^ (2)

Từ (1) và (2) ta có: H D E ^ = H A E ^ nên A, B, C đúng, D sai.

Đáp án: D

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có

góc A chung

=>ΔADB đồng dạng với ΔAEC

b: Xet ΔHEB vuôg tại E và ΔHDC vuông tại D có

góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC

=>HE/HD=HB/HC

=>HE*HC=HB*HD

c: ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC

=>góc ADE=góc ABC

C

C

a

1: Xét tứ giác AEDB có

\(\widehat{AEB}=\widehat{ADB}=90^0\)

=>AEDB là tứ giác nội tiếp đường tròn đường kính AB

Tâm I là trung điểm của AB

Bán kính là \(IA=\dfrac{AB}{2}\)

2: Xét ΔDBH vuông tại D và ΔDAC vuông tại D có

\(\widehat{DBH}=\widehat{DAC}\left(=90^0-\widehat{ACB}\right)\)

Do đó: ΔDBH đồng dạng với ΔDAC

=>DB/DA=DH/DC

=>\(DB\cdot DC=DA\cdot DH\)

3: ABDE là tứ giác nội tiếp

=>\(\widehat{ADE}=\widehat{ABE}=\widehat{ABN}\)

Xét (O) có

\(\widehat{ABN}\) là góc nội tiếp chắn cung AN

\(\widehat{AMN}\) là góc nội tiếp chắn cung AN

Do đó: \(\widehat{ABN}=\widehat{AMN}\)

=>\(\widehat{HDE}=\widehat{HMN}\)

mà hai góc này là hai góc ở vị trí đồng vị

nên DE//MN

Bài 2: 

a: Ta có: ΔAEH vuông tại E

mà EI là đường trung tuyến

nên IE=AH/2(1)

Ta có: ΔADH vuông tại D

mà DI là đường trung tuyến

nên DI=AH/2(2)

Từ (1) và (2) suy ra IE=ID

b: Xét tứ giác BEDC có 

\(\widehat{BEC}=\widehat{BDC}=90^0\)

Do đó: BEDC là tứ giác nội tiếp đường tròn đường kính BC

=>ME=MD

hay M nằm trên đường trung trực của ED(1)

Ta có: IE=ID

nên I nằm trên đường trung trực của ED(2)

Từ (1) và (2) suy ra IM là đường trung trực của ED

hay D đối xứng với E qua IM

a, Gọi T là trung điểm AH             

Tam giác AFH vuông tại F => AT=TF=TH (1)

Tam giác AEH vuông tại E => ET=AT=TH (2)

(1) và (2) => A,H,E,F cùng thuộc đường tròn tâm T

b, Tam giác EBC vuông tại E => EO=OC =>Tam giác EOC cân tại O => góc OEC = góc OCE  ( 1 )

Tam giác AEH đồng dạng tam giác ADC ( g-g ) => góc AHE = góc ACD ( 2 )

Theo chứng minh phần a => tam giác TEH cân tại E => góc TEH = góc THE ( 3 )

Từ (1),(2)và (3) => góc OEC = góc IEH

Ta có :góc IEO = IEH + HEO = HEO + OEC = 90 độ

=> IE vuông góc EO => OE là tiếp tuyến của ( T )