Tìm phương trình đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = 2 x - 1 2 - x
A. x = 1, y = 2
B. x = 2, y = -2
C. x = -2, y = 2
D. x = 2, y = 1
Xét các mệnh đề sau
(1). Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
(2). Đồ thị hàm số y = x + x 2 + x + 1 x có hai đường tiệm cận ngang và một đường tiệm cận đứng
(3). Đồ thị hàm số y = x - 2 x - 1 x 2 - 1 có một đường tiệm cận ngang và hai đường tiệm cận đứng.
Số mệnh đề đúng là:
A. 0
B. 3
C. 2
D. 1
Đáp án D
Đồ thị hàm số y = 1 2 x - 3 có hai đường tiệm cận đứng và một đường tiệm cận ngang
Đồ thị hàm số y = x + x 2 + x + 1 x có 1 tiệm cận đứng là x = 0
Mặt khác lim x → + ∞ y = x + x 2 + x + 1 x = lim x → + ∞ x + x + 1 x + 1 x 2 x = 0 nên đồ thị hàm số có 2 tiệm cận ngang
Xét hàm số y = x - 2 x - 1 x 2 - 1 = x - 2 x - 1 x + 2 x - 1 x 2 - 1 = x - 1 x + 2 x - 1 x - 1 x > 1 2 suy ra đồ thị không có tiệm cận đứng. Do đó có 1 mệnh đề đúng
Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 - x - x + 2 có phương trình lần lượt là
A. x=1,y=2
B. x=2,y=1
C. x=2,y= 1 2
D. x=2,y=-1
Phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 - 3 x x + 2 lần lượt là:
A. x = -2 và y = -3
B. y = -2 và x = -3
C. x = -2 và y = 1
D. x = 2 và y = 1
Chọn A.
Ta có  và
và 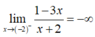 nên đồ thị hàm số có tiệm cận đứng là x = -2
nên đồ thị hàm số có tiệm cận đứng là x = -2
Ta có 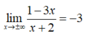 nên đồ thị hàm số có tiệm cận ngang là y = -3.
nên đồ thị hàm số có tiệm cận ngang là y = -3.
Phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 1 - 3 x x + 2 lần lượt là:
A.x=-2 và y=-3
B.y=-2 và x=-3
C.x=-2 và y=1
D.x=2 và y=1
Phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2 x − 1 1 − x lần lượt là:
A. x = -1; y= -2
B. x = -2; y = 1
C. x = 1; y = -2
D. x = 1; y = 2
Phương trình các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = 2 x − 1 1 − x lần lượt là
A. x = − 1 , y = − 2
B. x = − 2 , y = 1
C. x = 1 , y = − 2
D. x = 1 , y = 2
Đáp án C
Đồ thị hàm số có tiệm cận đứng là x = 1 tiệm cận ngang là y = 2
26. Tìm số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số y = \(\dfrac{\sqrt{x-1}}{x^2-3x+2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = 2 x - 1 x + 1
A. x= -1;y=2.
B. x=1;y= -2.
C. x=1/2;y= -1.
D. x= -1;y=1/2.
Tìm đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số y = 2 x - 1 x + 1
A. x = 1 2 , y = - 1
B. x = 1 , y = - 2
C. x = - 1 , y = 2
D. x = - 1 , y = 1 2