Hàm số y = 2 x + 3 x - 1 nghịch biến trên các khoảng:
A. R \ {1}
B. (-∞; 1) và (1; +∞)
C. (-∞; 2) và (2; +∞)
D. (-∞; -5) và (-5; +∞)
1. Đạo hàm của hàm số y= \(\left(x^3-5\right).\sqrt{x}\) bằng bao nhiêu?
2. Đạo hàm của hàm số y= \(\dfrac{1}{2}x^6-\dfrac{3}{x}+2\sqrt{x}\) là?
3. Hàm số y= \(2x+1+\dfrac{2}{x-2}\) có đạo hàm bằng?
1. \(y'=3x^2\sqrt{x}+\dfrac{x^3-5}{2\sqrt{x}}=\dfrac{7x^3-5}{2\sqrt{x}}\)
2. \(y'=3x^5+\dfrac{3}{x^2}+\dfrac{1}{\sqrt{x}}\)
3. \(y'=2-\dfrac{2}{\left(x-2\right)^2}\)
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Với các hàm số bậc nhất, hãy cho biết hàm số đó đồng biến hay nghịch biến? a)y=5-2x b)y=x√2-1. C)y=2(x+1)-2x. D)y=3(x-1)x. e)y=-2/3 x. f)y=x+ 1/x
Các hàm số a,b,e là các hàm số bậc nhất
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Trong các hàm số sau, hàm số nào không phải là hàm số bậc nhất? A. y= x-3/2 B. y= -7.4x/3 C. y= 1/2(x^2-1) D. y= (3-√2)x+5/2
\(y=\dfrac{1}{2}\left(x^2-1\right)\) không phải hàm số bậc nhất
Trong các hàm số sau, hàm số nào là hàm số chẵn, hàm số nào là hàm số lẻ:
\(y=5x^6;y=24x;y=-11x;y=\frac{2}{3}x^4;y=\sqrt{3}x^3;y=x^{10}\)
Cho hàm số y = f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) ( x - 2 ) 2 ( x - 3 ) 3 ( x + 5 ) 4 . Hỏi hàm số y = f ( x ) có mấy điểm cực trị?
A. 2
B. 3
C. 4
D. 5
Chọn A
f ' ( x ) đổi dấu khi x chạy qua -1 và 3 nên hàm số có 2 điểm cực trị.
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Trong các hàm số sau,hàm số nào là hàm số bậc nhất ? Với các hàm số bậc nhất , hãy cho biết hàm số đó đồng biến hay nghịch biến ?
a) y = 5 - 2x b) y = x√2 -1 c) y = 2(x+1) - 2x
d) y = 3(x-1) - x e) y = -2/3x f) y= x + 1/x
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
1. Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Xác định a, b?
a) y = 2x – 3
b) y = -7 – 6x
c) y = 2xbình2 + 1
d) y = 3(1 - x 2 )
e) y = 2(x + 1)
f) y = 3/x +2
a: Đây là hàm số bậc nhất
a=2; b=-3
b: Đây là hàm số bậc nhất
a=-6; b=-7
c: Đây ko là hàm số bậc nhất
Cho hàm số y= f( x) có đạo hàm f ' ( x ) = x 2 ( x - 9 ) ( x - 4 ) 2 . Xét hàm số y= g( x) =f( x2) Trong các phát biểu sau; tìm số phát biểu đúng
I. Hàm số y = g( x) đồng biến trên( 3; +∞)
II. Hàm số y= g(x) nghịch biến trên( -∞; -3)
III. Hàm số y= g( x) có 5 điểm cực trị
IV. m i n x ∈ R g ( x ) = f ( 9 )
A. 1
B. 2
C. 3
D. 4
Ta có
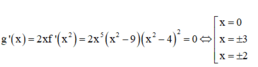
Bảng biến thiên của hàm số y= g( x)
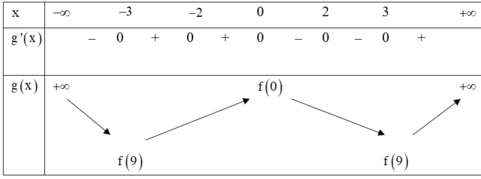
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.