giải phương trình
32x-1 + 3x-1(3x-7) - x+ 2 = 0
TN
Những câu hỏi liên quan
Giải các phương trình sau:a)
2
x
−
1
2
+
x
−
3
2
x
−
1
0
;
b)
3
−
2
x...
Đọc tiếp
Giải các phương trình sau:
a) 2 x − 1 2 + x − 3 2 x − 1 = 0 ;
b) 3 − 2 x 2 + 4 x 2 − 9 = 0 ;
c) 7 − x 2 + 2 3 x − 7 x − 3 = 0 ;
d) 4 3 x − 2 − 3 x − 2 3 = 0 .
Giải các phương trình sau:a)
3
x
−
2
x
+
1
0
; b)
x
2
+
2
2
x
−
1
0
;c)...
Đọc tiếp
Giải các phương trình sau:
a) 3 x − 2 x + 1 = 0 ; b) x 2 + 2 2 x − 1 = 0 ;
c) x + 3 2 x + 3 x − 5 = 0 ; d) x + 7 x + 6 2 − 4 x 3 = 0
Giải các phương trình sau:
a) x - 5(x - 2) = 6x
b) 23 + 3x2 - 32x = 48
c) (3x + 1)(x - 3)2 = (3x + 1)(2x - 5)2
d) 9x2 - 1 = (3x + 1)(4x + 1)
\(a,x-5\left(x-2\right)=6x\\ \Leftrightarrow x-5x+10-6x=0\\ \Leftrightarrow-10x+10=0\\ \Leftrightarrow x=1\\ b,2^3+3x^2-32x=48\\ \Leftrightarrow3x^2-32x+8=48\\ \Leftrightarrow3x^2-32x-40=0\)
Nghiệm xấu lắm bn
\(c,\left(3x+1\right)\left(x-3\right)^2=\left(3x+1\right)\left(2x-5\right)^2\\ \Leftrightarrow c,\left(3x+1\right)\left[\left(2x-5\right)^2-\left(x-3\right)^2\right]\\ \Leftrightarrow\left(3x+1\right)\left(2x-5-x+3\right)\left(2x-5+x-3\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(x-2\right)\left(3x-8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=2\\x=\dfrac{8}{3}\end{matrix}\right.\)
\(d,9x^2-1=\left(3x+1\right)\left(4x+1\right)\\ \Leftrightarrow\left(3x+1\right)\left(4x+1\right)-\left(3x-1\right)\left(3x+1\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(4x+1-3x+1\right)=0\\ \Leftrightarrow\left(3x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-2\end{matrix}\right.\)
Đúng 3
Bình luận (0)
\(b,2x^3+3x^2-32x-48=0\\ \Leftrightarrow\left(2x^3-8x^2\right)+\left(11x^2-44x\right)+\left(12x-48\right)=0\\ \Leftrightarrow2x^2\left(x-4\right)+11x\left(x-4\right)+12\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(2x^2+11x+12\right)=0\\ \Leftrightarrow\left(x-4\right)\left[\left(2x^2+8x\right)+\left(3x+12\right)\right]=0\\ \Leftrightarrow\left(x-4\right)\left[2x\left(x+4\right)+3\left(x+4\right)\right]=0\\ \Leftrightarrow\left(x-4\right)\left(2x+3\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{3}{2}\\x=-4\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Tìm k để các phương trình sau là phương trình bậc nhất ẩn x:a)
2
k
−
3
x
−
6
0
b)
k
2
+
3
x
+
7
0
c)
−
5
k...
Đọc tiếp
Tìm k để các phương trình sau là phương trình bậc nhất ẩn x:
a) 2 k − 3 x − 6 = 0 b) k 2 + 3 x + 7 = 0
c) − 5 k + 3 2 x − k 2 = 0 d) 3 kx − 5 k + 2 = 0
1.Giải các phương trình sau : a,7x+35=0 b, 8-x/x-7 -8 =1/x-7 2.giải bất phương trình sau : 18-3x(1-x)_< 3x^2-3x
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
Đúng 1
Bình luận (0)
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
Đúng 0
Bình luận (0)
1.
\(a,7x+35=0\\ \Rightarrow7x=-35\\ \Rightarrow x=-5\\ b,ĐKXĐ:x\ne7\\ \dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\\ \Leftrightarrow\dfrac{8-x}{x-7}-\dfrac{8\left(x-7\right)}{x-7}-\dfrac{1}{x-7}=0\\ \Leftrightarrow\dfrac{8-x-8x+56-1}{x-7}=0\\ \Rightarrow-9x+63=0\\ \Leftrightarrow-9x=-63\\ \Leftrightarrow x=7\left(ktm\right)\)
2.đề thiếu
Đúng 0
Bình luận (0)
Cho phương trình \(x^2\)+3x+m-1=0 ( x là ẩn)
a) giải ptr vs m=3
b) Định m để phương trình có 2 nghiệm x1,x2 thỏa mãn:
\(x^2_1.\left(x_1^4-1\right)+x_2.\left(32x^4_2-1\right)=3\)
\(x^2+3x+m-1=0\left(1\right)\)
Thay \(m=3\) vào \(\left(1\right)\)
\(\Rightarrow x^2+3x+3-1=0\)
\(\Rightarrow x^2+3x+2=0\)
\(\Rightarrow x^2+x+2x+2=0\)
\(\Rightarrow x\left(x+1\right)+2\left(x+1\right)=0\)
\(\Rightarrow\left(x+2\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+2=0\\x+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\x=-1\end{matrix}\right.\)
Vậy \(S=\left\{-2;-1\right\}\) khi \(m=3\)
Đúng 0
Bình luận (2)
Giải hệ phương trình:
\(\hept{\begin{cases}32x^3-48x^2+30x+\left(4y-7\right)\sqrt{1-y}=7\\3x+y-3=0\end{cases}}\)
Bây giờ a giải đc hệ này chưa ạ? Nếu giải đc r cho e xin lời giải đc ko ạ
Giải các phương trình sau:
x
+
1
3
+
3
2
x
+
1
4
2
x
+
3
x
+
1
6
+
7...
Đọc tiếp
Giải các phương trình sau: x + 1 3 + 3 2 x + 1 4 = 2 x + 3 x + 1 6 + 7 + 12 x 12
x + 1 3 + 3 2 x + 1 4 = 2 x + 3 x + 1 6 + 7 + 12 x 12 ⇔ x + 1 3 + 6 x + 3 4 = 5 x + 3 6 + 7 + 12 x 12
⇔ 4(x + 1) + 3(6x + 3) = 2(5x + 3) + 7 + 12x
⇔ 4x + 4 + 18x + 9 = 10x + 6 + 7 + 12x
⇔ 4x + 18x – 10x – 12x = 6 + 7 – 4 – 9
⇔ 0x = 0
Phương trình có vô số nghiệm.
Đúng 0
Bình luận (0)
Giải phương trình:
13
x
-
3
2
x
+
7
+
1
2
x...
Đọc tiếp
Giải phương trình: 13 x - 3 2 x + 7 + 1 2 x + 7 = 6 x - 3 x + 3
Điều kiện xác định: x ≠ ±3; x ≠ -7/2.
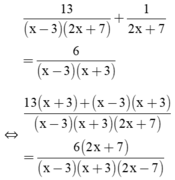
⇒ 13(x + 3) + (x – 3)(x + 3) = 6(2x + 7)
⇔ 13x + 39 + x2 – 9 = 12x + 42
⇔ x2 + x – 12 = 0
⇔ x2 +4x – 3x – 12 = 0
⇔ x(x + 4) – 3(x + 4) = 0
⇔ (x – 3)(x + 4) = 0
⇔ x – 3 = 0 hoặc x + 4 = 0
x – 3 = 0 ⇔ x = 3 (không thỏa mãn đkxđ)
x + 4 = 0 ⇔ x = -4 (thỏa mãn đkxđ).
Vậy phương trình có tập nghiệm S = {-4}.
Đúng 0
Bình luận (0)
Giải các phương trình:
\(a,x^2+2x-15=0\)
\(b,9x^2-1=\left(3x+1\right)\left(4x+1\right)\)
\(c,2x^3+3x^2-32x=48\)
\(a,\Leftrightarrow\left(x+5\right)\left(x-3\right)=0\Leftrightarrow x\in\left\{-5;3\right\}\)
\(b,\Leftrightarrow\left(3x-1\right)\left(3x+1\right)=\left(3x+1\right)\left(4x+1\right)\)
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\3x-1=4x+1\end{cases}}\)
\(c,\Leftrightarrow\left(2x^3-32x\right)+\left(3x^2-48\right)=0\Leftrightarrow2x\left(x-4\right)\left(x+4\right)+3\left(x-4\right)\left(x+4\right)\)
\(\Leftrightarrow\left(2x+3\right)\left(x+4\right)\left(x-4\right)=0\Leftrightarrow......\)
Đúng 0
Bình luận (0)