Tìm m để (P)y=-x2 + 4x-3 và (d) y=3m-1 cắt nhau tại hai điểm phân biệt nằm về phía trục Oy
ND
Những câu hỏi liên quan
Cho parabol (P): y = x 2 và đường thẳng d: y = (m + 2)x – m – 1. Tìm m để d cắt (P) tại hai điểm phân biệt nằm về hai phía trục tung
A. m < −1
B. m < −2
C. m > −1
D. −2 < m < −1
Phương trình hoành độ giao điểm của d và (P): x 2 = (m + 2)x – m – 1
↔ x 2 − (m + 2)x + m + 1 = 0 (1)
(d) cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm phân biệt trái dấu ↔ ac < 0 ↔ m + 1 < 0
↔ m < −1
Vậy m < −1
Đáp án: A
Đúng 0
Bình luận (0)
Cho đường thẳng d: y 2x − 5 và parabol (P):
y
(
m
–
1
)
x
2
(m ≠ 0) . Tìm m để d và (P) cắt nhau tại hai điểm A và B phân biệt và cùng nằm về một phía đối với trục tung. A. m 1 B.
-
2
3
m
1
C.
2
3
m...
Đọc tiếp
Cho đường thẳng d: y = 2x − 5 và parabol (P): y = ( m – 1 ) x 2 (m ≠ 0) . Tìm m để d và (P) cắt nhau tại hai điểm A và B phân biệt và cùng nằm về một phía đối với trục tung.
A. m > 1
B. - 2 3 < m < 1
C. 2 3 < m < 1
D. m < - 2 3
a, Giải hệ phương trình:
x
+
1
y
-
1
x
y
-
1...
Đọc tiếp
a, Giải hệ phương trình: x + 1 y - 1 = x y - 1 x - 3 y - 3 = x y - 3
b, Trên mặt phẳng tọa độ Oxy, cho prabol (P): y = x 2 và đường thẳng d: y = 2 x + m 2 - 2 m . Tìm các giá trị của m để d cắt (P) cắt tại hai điểm phân biệt nằm về hai phía của trục tung Oy
a, Biến đổi hệ phương trình ban đầu ta được hệ x - y = 0 3 x + 3 y = 12
Từ đó tìm được x = 2, y = 2
b, Phương trình hoành độ giao điểm của d và (p):
x 2 - 2 x - m 2 + 2 m = 0 (1)
d cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung Oy <=> (1) có hai nghiệm trái dấu. Từ đó tìm được 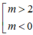
Kết luận 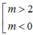
Đúng 0
Bình luận (0)
Tìm tham số m để đường thẳng d: y = (m – 2)x + 3m và parabol (P): y = x 2 cắt nhau tại hai điểm phân biệt nằm bên trái trục tung
A. m < 3
B. m > 3
C. m > 2
D. m > 0
Phương trình hoành độ giao điểm x 2 = (m – 2)x + 3m ↔ x 2 − (m – 2)x − 3m = 0 (*)
Đường thẳng d cắt (P) tại hai điểm phân biệt nằm hai phía trục tung
↔ Phương trình (*) có hai nghiệm trái dấu
↔ ac < 0 ↔ −3m < 0 ↔ m > 0
Đáp án: D
Đúng 0
Bình luận (0)
Cho parabol (P): y x2 và đường thẳng (d): y mx - m + 1, m là tham số.a)Với m 3 hãy tìm tọa độ giao điểm của (P) và (d)b) T ìm m để (d) cắt (P) tại 2 điểm nằm về hai phía của trục tung.c)Tìm m để (d) cắt (P) tại 2 điểm phân biệt cùng có hoành độ dương.d)Tìm m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 thoả mãn x1 x2 2
Đọc tiếp
Cho parabol (P): y = x2 và đường thẳng (d): y = mx - m + 1, m là tham số.
a)Với m = 3 hãy tìm tọa độ giao điểm của (P) và (d)
b) T ìm m để (d) cắt (P) tại 2 điểm nằm về hai phía của trục tung.
c)Tìm m để (d) cắt (P) tại 2 điểm phân biệt cùng có hoành độ dương.
d)Tìm m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ x1, x2 thoả mãn x1 < x2 < 2
a: Thay m=3 vào (d), ta được:
y=3x-3+1=3x-2
Tọa độ giao điểm của (P) và (d) là:
\(\left\{{}\begin{matrix}x^2-3x+2=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-2\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;1\right);\left(2;4\right)\right\}\)
b: Phương trình hoành độ giao điểm là:
\(x^2-mx+m-1=0\)
Để (P) cắt (d) tại hai điểm về hai phía của trục tung thì m-1<0
hay m<1
c: Để (P) cắt (d) tại hai điểm phân biệt có hoành độ dương thì
\(\left\{{}\begin{matrix}\left(-m\right)^2-4\left(m-1\right)>0\\m>0\\m-1>0\end{matrix}\right.\Leftrightarrow m>1\)
Đúng 1
Bình luận (0)
Có bao nhiêu số nguyên m thỏa mãn -100 ≤ m ≤ 200 để đổ thị hàm số y = 2x + 5 và y = x^2 + m + 1 cắt nhau tại hai điểm phân biệt nằm về hai phía trục Oy
Phương trình hoành độ giao điểm:
\(x^2+m+1=2x+5\)
\(\Leftrightarrow x^2-2x+m-4=0\) (1)
Hai đồ thị cắt nhau tại 2 điểm nằm về 2 phía Oy khi và chỉ khi (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow ac=m-4< 0\)
\(\Leftrightarrow m< 4\)
\(\Rightarrow\) Có \(3-\left(-100\right)+1=104\) số nguyên thỏa mãn
Đúng 0
Bình luận (0)
Cho đường thẳng d: y −3x + 1 và parabol (P):
y
m
x
2
(m ≠ 0) . Tìm m để d và (P) cắt nhau tại hai điểm A và B phân biệt và cùng nằm về một phía đối với trục tung. A.
m
-
9
4
B.
-
9
4
m
0
C. m 0 D.
m
9...
Đọc tiếp
Cho đường thẳng d: y = −3x + 1 và parabol (P): y = m x 2 (m ≠ 0) . Tìm m để d và (P) cắt nhau tại hai điểm A và B phân biệt và cùng nằm về một phía đối với trục tung.
A. m > - 9 4
B. - 9 4 < m < 0
C. m < 0
D. m > 9 4
Cho parabol (P): y = x2 và đường thẳng (d): y = (2m+1)x - m2 - m. Tìm m để (d) cắt (P) tại hai điểm phân biệt A, B sao cho A, B nằm ở hai phía trục tung.
PTHĐGĐ là:
x^2-(2m+1)x+m^2+m=0
Để (d) cắt (P) tại hai điểm phân biệt nằm về hai phía trục tung thì m^2+m<0
=>-1<m<0
Đúng 1
Bình luận (0)
Tìm tham số m để đường thẳng d: y mx + m + 1 và parabol (P):
y
x
2
cắt nhau tại hai điểm phân biệt nằm bên trái trục tung. A.
m
0
m
≠
-
2
B. ...
Đọc tiếp
Tìm tham số m để đường thẳng d: y = mx + m + 1 và parabol (P): y = x 2 cắt nhau tại hai điểm phân biệt nằm bên trái trục tung.
A. m < 0 m ≠ - 2
B. m < - 1 m ≠ - 2
C. m > −1
D. m ≥ −2





