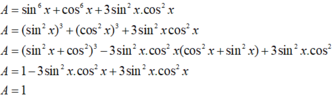sin6x + cos6x + 3sin2xcos2x
H24
Những câu hỏi liên quan
N = sin6x + cos6x + 3sin2xcos2x
Tính đạo hàm của hàm số y = sin 6 x + cos 6 x + 3 sin 2 x cos 2 x
A.. 1
B. 0
C. 2
D. 3
Tính giá trị của biểu thức A = sin6x + cos6x + 3sin2xcos2x.
A. A = 1
B. A = 2
C. A = 3
D. A = 4
Tìm đạo hàm của hàm số
y
sin
6
x
+
c
os
6
x
+
3
sin
2
x
c
os
2
x
.
A. 1 B. 0 C. 2 D. 3
Đọc tiếp
Tìm đạo hàm của hàm số y = sin 6 x + c os 6 x + 3 sin 2 x c os 2 x .
A. 1
B. 0
C. 2
D. 3
Đáp án B
Ta có y = sin 6 x + cos 6 x + 3 sin 2 x c os 2 x = 1 − 3 4 sin 2 2 x + 3 4 sin 2 2 x = 1 ⇒ y ' = 0.
Đúng 0
Bình luận (0)
Chứng minh rằng hàm số y = sin6x + cos6x + 3sin2xcos2x có đạo hàm bằng 0.
Cho hàm số f(x) sin6x + cos6x + 3sin2xcos2x. Khi đó f’(x) có giá trị bằng bao nhiêu? A. 1. B. 2. C. 0. D. -1.
Đọc tiếp
Cho hàm số f(x) = sin6x + cos6x + 3sin2xcos2x. Khi đó f’(x) có giá trị bằng bao nhiêu?
A. 1.
B. 2.
C. 0.
D. -1.
Chọn C.
f'(x) = 6sin5xcosx – 6cos5xsinx + 3(2sinxcos3x – 2cosxsin3x)
= 6sinxcosx(sin4x – cos4x + cos2x – sin2x)
= 6sinxcosx(sin2x – cos2x + cos2x – sin2x) = 0.
Đúng 0
Bình luận (0)
Cho 0 x
90
0
. Chứng minh các đẳng thức sau:a,
sin
4
x
+
cos
4
x
1
-
2
sin
2
x
cos...
Đọc tiếp
Cho 0 <x< 90 0 . Chứng minh các đẳng thức sau:
a, sin 4 x + cos 4 x = 1 - 2 sin 2 x cos 2 x
b, sin 6 x + cos 6 x = 1 - 3 sin 2 x cos 2 x
a, Ta có: sin 4 x + cos 4 x = sin 2 x + cos 2 x 2 - 2 sin 2 x . cos 2 x = 1 - 2 sin 2 x . cos 2 x
b, Ta có: sin 6 x + cos 6 x = sin 2 x + cos 2 x 3 - 3 sin 2 x cos 2 x sin 2 x + cos 2 x = 1 - 3 sin 2 x cos 2 x
Đúng 0
Bình luận (0)
1) Giai
a) cos6x + sin6x
Rút gọn biểu thức : P=\(\dfrac{1+sin6x-cos6x}{1+sin6x+cos6x}\) sau đó tính P khi x= \(\dfrac{7\pi}{4}\)
\(P=\dfrac{1+2sin3xcos3x-\left(1-2sin^23x\right)}{1+2sin3xcos3x+2cos^2x-1}=\dfrac{2sin3xcos3x+2sin^23x}{2sin3xcos3x+2cos^23x}=\dfrac{sin3x}{cos3x}=tan3x\)
\(x=\dfrac{7\pi}{4}\Rightarrow P=tan\dfrac{21\pi}{4}=tan\dfrac{\pi}{4}=1\)
Đúng 0
Bình luận (0)