Xét tính đúng sai
∃x∈N,(x2+x) không ⋮2
xét tính đúng sai của mệnh đề :∃xϵQ;x>x2
Mệnh đề này là mệnh đề đúng
Ví dụ với \(x=\dfrac{1}{2}\) thì \(x^2=\dfrac{1}{4}\Rightarrow\dfrac{1}{2}>\dfrac{1}{4}\) đúng
Mệnh đề này đúng
Vd: \(x=\dfrac{1}{4}\) thì \(x=\dfrac{1}{4}>x^2=\dfrac{1}{16}\)
Phát biểu thành lời, xét tính đúng sai và lập mệnh đề phủ định của các mệnh đề sau:
a/ ∃ x ∈ R : x2 = -1
b/∀ x ∈ R : x2 +x +2 ≠0
giup mình voi . Mình cần gấp
Lời giải:
a. Mệnh đề sai, vì $x^2\geq 0>-1$ với mọi $x\in\mathbb{R}$ theo tính chất bình phương 1 sosos.
Mệnh đề phủ định: $\forall x\in\mathbb{R}, x^2\neq -1$
b. Mệnh đề đúng, vì $x^2+x+2=(x+0,5)^2+1,75>0$ với mọi $x\in\mathbb{R}$ nên $x^2+x+2\neq 0$ với mọi $x\in\mathbb{R}$
Mệnh đề phủ định: $\exists x\in\mathbb{R}| x^2+x+2=0$
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∃ x ∈ Q : x2 = 2
B: “∃ x ∈ Q : x2 = 2”.
B− : “∀ x ∈ Q : x2 ≠ 2”
B− đúng.
Lưu ý: √2 là số vô tỷ.
Phát biểu thành lời các mệnh đề sau và xét tính đúng sai của chúng. ∃ x ∈ R : x 2 + x + 1 > 0
Có một số thực x, mà x 2 + x + 1 > 0 (mệnh đề đúng).
Phát biểu thành lời mỗi mệnh đề sau và xét tính đúng sai của nó. ∀ x ∈ R : x2 > 0
Bình phương của mọi số thực đều dương.
– Mệnh đề này sai vì nếu x = 0 thì x2 = 0.
Sửa cho đúng: ∀ x ∈ R : x2 ≥ 0.
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó x =2 là một nghiệm của phương trình x 2 - 4 x - 2 = 0
Mệnh đề sai.
Phủ định là "x = 2 không là nghiệm của phương trình" 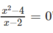 mệnh đề này đúng.
mệnh đề này đúng.
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó. x =2 là một nghiệm của phương trình x 2 - 4 x - 2 = 0
Mệnh đề sai.
Phủ định là "x = 2 không là nghiệm của phương trình" 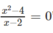 mệnh đề này đúng.
mệnh đề này đúng.
Cho mênh đề “ ∀ x ∈ ℝ , x 2 + x ≥ − 1 4 ”. Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó
A. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≥ − 1 4 " Đây là mệnh đề đúng
B. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≤ − 1 4 " Đây là mệnh đề đúng
C. A ¯ : " ∃ x ∈ ℝ , x 2 + x < − 1 4 " Đây là mệnh đề đúng
D. A ¯ : " ∃ x ∈ ℝ , x 2 + x ≥ − 1 4 " Đây là mệnh đề sai
Nhận xét sự đúng, sai của kết quả sau :
x2 + 2xy + 4y2 = (x + 2y)2
Kết quả trên sai.
Ta có: (x + 2y)2 = x2 + 2.x.2y + 4y2 = x2 + 4xy + 4y2 ≠ x2 + 2xy + 4y2.
Lập mệnh đề phủ định của các mệnh đề sau và xét tính đúng, sai của nó: ∃ x ∈ R: 3x = x2 + 1
D: “∃ x ∈ R: 3x = x2 + 1”
D− : “∀ x ∈ R ; 3x ≠ x2 + 1”
D− sai vì với 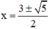
D− thỏa mãn: