(2x-5)2020+(3y+4)2022 < hoặc = 0
Tìm đa thức M biết rằng:M+(5x^2-2xy)=6x^2+9xy-y^2.Tính giá trị của M khi x,y thỏa mãn (2x-5)^2020+(3y+4)^2022 <hoặc=0
M=6x^2+9xy-y^2-5x^2+2xy=x^2+11xy-y^2
(2x-5)^2020+(3y+4)^2022<=0
=>x=5/2 và y=-4/3
M=25/4+11*5/2*(-4/3)-16/9=-1159/36
(1/3-2X)^2020+(3Y-X)^2022 lớn hơn hoặc bằng 0 chứng minh 1/x+1/y=24
giúp mk với ah
Sửa: \(\left(\dfrac{1}{3}-2x\right)^{2020}+\left(3y-x\right)^{2022}\le0\)
Mà \(\left(\dfrac{1}{3}-2x\right)^{2020}+\left(3y-x\right)^{2022}\ge0\) với mọi x,y
Do đó \(\left\{{}\begin{matrix}\dfrac{1}{3}-2x=0\\3y-x=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{6}\\y=\dfrac{1}{18}\end{matrix}\right.\)
\(\Leftrightarrow\dfrac{1}{x}+\dfrac{1}{y}=6+18=24\)
(3y+5)^2020+|2x-5|+(3z-4)^2022
Tìm x,y:
(2x-5)2020+(3y+4)2018 < hoặc = 0
\(\left(2x-5\right)^{2020}+\left(3y+4\right)^{2018}\le0\left(1\right)\)
Ta có: \(\hept{\begin{cases}\left(2x-5\right)^{2020}\ge0;\forall x,y\\\left(3y+4\right)^{2018}\ge0;\forall x,y\end{cases}}\)\(\Rightarrow\left(2x-5\right)^{2020}+\left(3y+4\right)^{2018}\ge0;\forall x,y\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow\left(2x-5\right)^{2020}+\left(3y+4\right)^{2018}=0\)
\(\Leftrightarrow\hept{\begin{cases}\left(2x-5\right)^{2020}=0\\\left(3y+4\right)^{2018}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\y=\frac{-4}{3}\end{cases}}\)
Vậy...
Tìm x,y biết:
(2x-5)2020+(5y+1)2022 < hoặc = 0
Vì \(\left(2x-5\right)^{2020}\ge0\forall x\); \(\left(5y+1\right)^{2022}\ge0\forall y\)
\(\Rightarrow\left(2x-5\right)^{2020}+\left(5y+1\right)^{2022}\ge0\forall x,y\)
mà \(\left(2x-5\right)^{2020}+\left(5y+1\right)^{2022}\le0\)( giả thuyết )
Dấu " = " xảy ra \(\Leftrightarrow\hept{\begin{cases}2x-5=0\\5y+1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x=5\\5y=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\y=\frac{-1}{5}\end{cases}}\)
Vậy \(x=\frac{5}{2}\)và \(y=\frac{-1}{5}\)
( 2x - 5 )2020 + ( 5y + 1 )2022 ≤ 0
Ta có : ( 2x - 5 )2020 ≥ 0 ∀ x
( 5y + 1 )2022 ≥ 0 ∀ y
=> ( 2x - 5 )2 + ( 5y + 1 )2022 ≥ 0 ∀ x, y
Kết hợp với đề bài => Chỉ xảy ra trường hợp ( 2x - 5 )2020 + ( 5y + 1 )2022 = 0
Khi đó \(\hept{\begin{cases}2x-5=0\\5y+1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{5}{2}\\y=-\frac{1}{5}\end{cases}}\)
Tìm x,y:
(2x-5)2020+(3y+4)2018 < hoặc = 0
\(\left(2x-5\right)^{2020}+\left(3y+4\right)^{2018}\le0\)
Ta có:
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2020}\ge0\\\left(3y+4\right)^{2018}\ge0\end{matrix}\right.\forall xy.\)
\(\Rightarrow\left(2x-5\right)^{2020}+\left(3y+4\right)^{2018}\ge0\) \(\forall xy.\)
Mà \(\left(2x-5\right)^{2020}+\left(3y+4\right)^{2018}\le0.\)
\(\Rightarrow\left(2x-5\right)^{2020}+\left(3y+4\right)^{2018}=0\)
\(\Rightarrow\left(2x-5\right)+\left(3y+4\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}2x-5=0\\3y+4=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}2x=5\\3y=-4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=5:2\\y=\left(-4\right):3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\frac{5}{2}\\y=-\frac{4}{3}\end{matrix}\right.\)
Vậy \(\left(x;y\right)\in\left\{\frac{5}{2};-\frac{4}{3}\right\}.\)
Chúc bạn học tốt!
Ta có:
(2x+5)2020 ≥ 0 với ∀ x
(3y+4)2018 ≥ 0 với ∀ y
⇒ (2x+5)2020 + (3y+4)2018 ≥ 0 với ∀ x, y
Mà (2x+5)2020 + (3y+4)2018 ≤ 0
⇒ (2x+5)2020 + (3y+4)2018 = 0
⇒ \(\left[{}\begin{matrix}\left(2x+5\right)^{2020}=0\\\left(3y+4\right)^{2018}=0\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}2x+5=0\\3y+4=0\end{matrix}\right.\)
⇒ \(\left[{}\begin{matrix}2x=-5\\3y=-4\end{matrix}\right.\) ⇒ \(\left[{}\begin{matrix}x=\frac{-5}{2}\\y=\frac{-4}{3}\end{matrix}\right.\)
Vậy...
Học tốt❤
tìm x,y biết ( 2x - 8 ) mũ 2000 + ( 3y + 4 ) mũ 2022 bé hơn hoặc bằng 0
Ta có: \(\left(2x-8\right)^{2000}+\left(3y+4\right)^{2022}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x-8=0\\3y+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=8\\3y=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=-\dfrac{4}{3}\end{matrix}\right.\)
Tìm x , y biết: (2x -5)2022 + (3y +4)2024 ≤ 0
Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
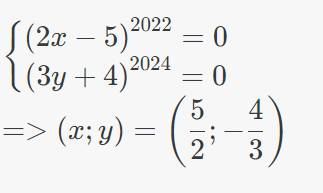 Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Tìm đa thức M biết rằng:M+(5x^2-2xy)=6x^2+9xy-y^2.Tính giá trị của M khi x,y thỏa mãn (2x-5)^2018+(3y+4)^2020 <hoặc=0
\(\left(2x-5\right)^{2018}+\left(3y+4\right)^{2020}\le0\\ \Leftrightarrow\left(2x-5\right)^{2018}+\left(3y+4\right)^{2020}=0\\ \Leftrightarrow\left\{{}\begin{matrix}\left(2x-5\right)^{2018}=0\\\left(3y+4\right)^{2020}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{2}\\y=-\dfrac{4}{3}\end{matrix}\right.\\ \Leftrightarrow M=6x^2+9xy-y^2-5x^2+2xy=x^2+11xy-y^2\\ \Leftrightarrow M=\dfrac{25}{4}-11\cdot\dfrac{4}{3}\cdot\dfrac{5}{2}-\dfrac{16}{9}=\dfrac{25}{4}-\dfrac{110}{3}-\dfrac{16}{9}=-\dfrac{1159}{36}\)