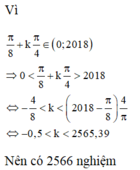Pt \(2sin2x+\sqrt{2}=0\) có bao nhiêu nghiệm thuộc khoảng \(\left(0;\pi\right)\)
JE
Những câu hỏi liên quan
Phương trình 2 sin 2 x + 3 sin x cos x + cos 2 x = 0 có bao nhiêu nghiệm thuộc (-π/2;π)
A. 0
B. 1
C. 2
D. 4
Tìm m để phương trình sau có 5 nghiệm phân biệt thuộc khoảng \(\left(-\dfrac{\pi}{2};3\pi\right)\)
2sin2x - (5m + 1)sinx + 2m2 + 2m = 0
Từ đường tròn lượng giác, trên \(\left(-\dfrac{\pi}{2};3\pi\right)\):
- Nếu \(0< t< 1\) thì \(sinx=t\) có 4 nghiệm
- Nếu \(-1< t< 0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=0\) thì \(sinx=t\) có 3 nghiệm
- Nếu \(t=1\) thì \(sinx=t\) có 2 nghiệm
- Nếu \(t=-1\) thì \(sinx=t\) có 1 nghiệm
Do đó pt đã cho có 5 nghiệm pb trong khoảng đã cho khi:
\(2t^2-\left(5m+1\right)t+2m^2+2m=0\) có 2 nghiệm pb thỏa mãn:
- TH1: \(\left\{{}\begin{matrix}t_1=-1\\0< t_2< 1\end{matrix}\right.\)
- TH2: \(\left\{{}\begin{matrix}-1< 0< t_1\\t_2=1\end{matrix}\right.\)
- TH3: \(\left\{{}\begin{matrix}t_1=0\\t_2=1\end{matrix}\right.\)
Về cơ bản, chỉ cần thay 1 nghiệm bằng 0 hoặc 1 rồi kiểm tra nghiệm còn lại có thỏa hay ko là được
Đúng 1
Bình luận (1)
1. Pt: sin^22x-2cos^2x+frac{3}{4}0 có nghiệm là?
2. Số nghiệm của pt: 2cos2x+2cosx-sqrt{2}0 thỏa đk: frac{-pi}{2} x frac{5pi}{2}?
3. Số nghiệm của pt: 2tanx-2cotx-30 trong khoảng: left(frac{-pi}{2};piright) là?
4. Nghiệm âm lớn nhất của pt: frac{sqrt{3}}{sin^2x}3cotx+sqrt{3} là?
5. Tổng các nghiệm của pt: sqrt{3}tan^2x-left(3+sqrt{3}right)tanx+30 trong: left(-2019pi;2019piright) thuộc khoảng nào trong các khoảng sau?
a. left(-infty;-3right) b. left(-3;5right) c. (5;20) d. left(20;+in...
Đọc tiếp
1. Pt: \(sin^22x-2cos^2x+\frac{3}{4}=0\) có nghiệm là?
2. Số nghiệm của pt: \(2cos2x+2cosx-\sqrt{2}=0\) thỏa đk: \(\frac{-\pi}{2}< x< \frac{5\pi}{2}\)?
3. Số nghiệm của pt: \(2tanx-2cotx-3=0\) trong khoảng: \(\left(\frac{-\pi}{2};\pi\right)\) là?
4. Nghiệm âm lớn nhất của pt: \(\frac{\sqrt{3}}{sin^2x}=3cotx+\sqrt{3}\) là?
5. Tổng các nghiệm của pt: \(\sqrt{3}tan^2x-\left(3+\sqrt{3}\right)tanx+3=0\) trong: \(\left(-2019\pi;2019\pi\right)\) thuộc khoảng nào trong các khoảng sau?
a. \(\left(-\infty;-3\right)\) b. \(\left(-3;5\right)\) c. (5;20) d. \(\left(20;+\infty\right)\)
6. Pt: 1 + sinx - cosx - sin2x = 0 có bao nhiêu nghiệm trên: \(\left[0;\frac{\pi}{2}\right]\)?
7. Tổng các nghiệm của pt: \(sinxcosx+\left|cosx+sinx\right|=1\) trên \(\left(0;2\pi\right)\) là?
1.
\(\Leftrightarrow1-cos^22x-2\left(\frac{1+cos2x}{2}\right)+\frac{3}{4}=0\)
\(\Leftrightarrow-cos^22x-cos2x+\frac{3}{4}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\frac{1}{2}\\cos2x=-\frac{3}{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow2x=\pm\frac{\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\frac{\pi}{6}+k\pi\)
2.
\(2\left(2cos^2x-1\right)+2cosx-\sqrt{2}=0\)
\(\Leftrightarrow4cos^2x+2cosx-2-\sqrt{2}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=\frac{\sqrt{2}}{2}\\cosx=-\frac{1+\sqrt{2}}{2}< -1\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k2\pi\\x=-\frac{\pi}{4}+l2\pi\end{matrix}\right.\) mà \(-\frac{\pi}{2}< x< \frac{5\pi}{2}\Rightarrow\left\{{}\begin{matrix}-\frac{\pi}{2}< \frac{\pi}{4}+k2\pi< \frac{5\pi}{2}\\-\frac{\pi}{2}< -\frac{\pi}{4}+l2\pi< \frac{5\pi}{2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}k=0;1\\l=0;1\end{matrix}\right.\) \(\Rightarrow x=\left\{\frac{\pi}{4};\frac{9\pi}{4};-\frac{\pi}{4};\frac{7\pi}{4}\right\}\)
Có 4 nghiệm
Đúng 0
Bình luận (0)
3. ĐKXĐ: ...
\(2tanx-\frac{2}{tanx}-3=0\)
\(\Leftrightarrow2tan^2x-3tanx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=-\frac{1}{2}\\tanx=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arctan\left(-\frac{1}{2}\right)+k\pi\\x=arctan\left(2\right)+k\pi\end{matrix}\right.\)
Có 3 nghiệm trong khoảng đã cho \(x=arctan\left(-\frac{1}{2}\right);x=arctan\left(-\frac{1}{2}\right)+\pi;x=arctan\left(2\right)\)
Đúng 0
Bình luận (0)
4. ĐKXĐ: ...
\(\Leftrightarrow\sqrt{3}\left(1+cot^2x\right)=3cotx+\sqrt{3}\)
\(\Leftrightarrow cot^2x-\sqrt{3}cotx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cotx=0\\cotx=\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{6}+k\pi\end{matrix}\right.\)
Nghiệm âm lớn nhất của pt là \(x=-\frac{\pi}{2}\)
5. ĐKXĐ; ...
\(\Leftrightarrow tan^2x-\left(1+\sqrt{3}\right)tanx+\sqrt{3}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}tanx=1\\tanx=\sqrt{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{3}+l\pi\end{matrix}\right.\)
\(\left\{{}\begin{matrix}-2019\pi< \frac{\pi}{4}+k\pi< 2019\pi\\-2019\pi< \frac{\pi}{3}+l\pi< 2019\pi\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}-2019\le k\le2018\\-2019\le l\le2018\end{matrix}\right.\)
Tổng các nghiệm: \(2.\left(-2019\pi\right)+4038\left(\frac{\pi}{3}+\frac{\pi}{4}\right)=-\frac{3365\pi}{2}< -3\)
Đáp án A đúng
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Phương trình \(sin\left(x^2-5x\right)=\dfrac{-\sqrt{3}}{2}\) có bao nhiêu nghiệm thuộc \(\left[0;\dfrac{\pi}{2}\right]\)
Tìm nghiệm của pt:
1) \(2cos2x+\sqrt{2}cos\frac{\pi}{4}=0\) thuộc khoảng (0;2π)
2) \(sin4x-cos4x+\sqrt{2}cos\left(4x-\frac{\pi}{4}\right)=\sqrt{6}\) thuộc khoảng (-π;5π)
1.
\(\Leftrightarrow2cos2x+\sqrt{2}.\frac{\sqrt{2}}{2}=0\)
\(\Leftrightarrow cos2x=-\frac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k\pi\\x=-\frac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\frac{\pi}{3};\frac{4\pi}{3};\frac{2\pi}{3};\frac{5\pi}{3}\right\}\)
2.
\(\Leftrightarrow sin4x-cos4x+sin4x+cos4x=\sqrt{6}\)
\(\Leftrightarrow2sin4x=\sqrt{6}\)
\(\Leftrightarrow sin4x=\frac{\sqrt{6}}{2}>1\)
Pt vô nghiệm
Đúng 0
Bình luận (0)
Cho pt : \(\left(x^2-2x+3\right)^2+2\left(3-m\right)\left(x^2-2x+3\right)+m^2-6m=0\). Có bao nhiêu giá trị nguyên của m thuộc \([-10;10]\) có nghiệm ?
Đặt \(t=x^2-2x+3\left(t\ge2\right)\)
Phương trình trở thành \(f\left(t\right)=t^2+2\left(3-m\right)t+m^2-6m=0\left(1\right)\)
Phương trình \(\left(1\right)\) có nghiệm \(t_1\ge t_2\ge2\) khi:
\(\left\{{}\begin{matrix}\Delta'\ge0\\\dfrac{t_1+t_2}{2}\ge2\\1.f\left(2\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3-m\right)^2-m^2+6m\ge0\\m-3\ge2\\m^2-10m+16\ge0\end{matrix}\right.\)
Giải ra tập giá trị của m rồi lấy các giá trị thuộc \(\left[-10;10\right]\)
Đúng 3
Bình luận (0)
Bất phương trình \(x^2-2\left|x-1\right|+2>0\) có bao nhiêu nghiệm nguyên thuộc khoảng (-20; 30)
Phương trình
2
cos
2
x
+
2
cos
2
2
x
+
2
cos
2
3
x
-3cos4x(2sin2x+1)có bao nhiêu nghiệm thuộc khoảng (0;2018) A. 2565 B. 2566 C. 2567 D. 2568
Đọc tiếp
Phương trình 2 cos 2 x + 2 cos 2 2 x + 2 cos 2 3 x -3=cos4x(2sin2x+1)có bao nhiêu nghiệm thuộc khoảng (0;2018)
A. 2565
B. 2566
C. 2567
D. 2568
Pt \(sinx\left(3cosx-2\right)=0\) có bao nhiêu nghiệm thuộc khoảng \(\left(0;3\pi\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\cosx=\frac{2}{3}\end{matrix}\right.\)
Từ đường tròn lượng giác ta thấy \(sinx=0\) có 4 nghiệm và \(cosx=\frac{2}{3}\) có 3 nghiệm
Vậy pt có 7 nghiệm thuộc khoảng đã cho
Đúng 0
Bình luận (0)