Khi phương trình -x^2+2x+2m-1=0 có hai nghiệm phân biệt, hãy biểu diễn tích hai nghiệm đó theo m.
H24
Những câu hỏi liên quan
Biết phương trình x^2+(m-1)x-2=0 có hai nghiệm phân biệt. Biểu diễn tổng hai nghiệm đó theo m.
GHJHGJYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY
\(x_1=\frac{-\left(m-1\right)+\sqrt{\left(m-1\right)^2+8}}{2a}\)
\(x_2=\frac{-\left(m-1\right)-\sqrt{\left(m-1\right)^2+8}}{2a}\)
a)Cho phương trình : (m+2)x^2 - (2m-1)x-3+m0 tìm điều kiện của m để phương trình có hai nghiệm phân biệt x1, x2 sao cho nghiệm này gấp đôi nghiệm kiab)Cho phương trình bậc hai: x^2-mx+m-10. Tìm m để phương trình có hai nghiệm x1;x2 sao cho biểu thức R2x1x2+3/x1^2+x2^2+2(1+x1x2) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đóc)Định m để hiệu hai nghiệm của phương trình sau đây bằng 2mx^2-(m+3)x+2m+10Mọi người giúp em giải chi tiết ra với ạ. Em cảm ơn!
Đọc tiếp
a)Cho phương trình : (m+2)x^2 - (2m-1)x-3+m=0 tìm điều kiện của m để phương trình có hai nghiệm phân biệt x1, x2 sao cho nghiệm này gấp đôi nghiệm kia
b)Cho phương trình bậc hai: x^2-mx+m-1=0. Tìm m để phương trình có hai nghiệm x1;x2 sao cho biểu thức R=2x1x2+3/x1^2+x2^2+2(1+x1x2) đạt giá trị lớn nhất. Tìm giá trị lớn nhất đó
c)Định m để hiệu hai nghiệm của phương trình sau đây bằng 2
mx^2-(m+3)x+2m+1=0
Mọi người giúp em giải chi tiết ra với ạ. Em cảm ơn!
Cho phương trình (2m - 1)
x
2
- 2(m + 4)x + 5m + 2 0 ( m
≠
1
2
)Khi phương trình có nghiệm
x
1
,
x
2
hãy tính tổng S và tích P của hai nghiệm theo m
Đọc tiếp
Cho phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
Khi phương trình có nghiệm x 1 , x 2 hãy tính tổng S và tích P của hai nghiệm theo m
Phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
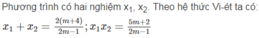
Đúng 0
Bình luận (0)
a Tìm m để phương trình x^2-left(2m+1right)x+m^2+10 có hai nghiệm phân biệt trong đó nghiệm nàygấp đôi nghiệm kiab Tìm m để phương trình x^2-2mx+m-30 có hai nghiệm x_1,x_2 thỏa mãn x_1+2x_2 1c Tìm m để phương trình x^2-2mx+left(m-1right)^30 có hai nghiệm trong đó nghiệm này là bìnhphương của nghiệm kia .d Tìm m để phương trình 2x^2-left(m+1right)x+m+30 có hai nghiệm sao cho hiệu hai nghiệm bằng 1.
Đọc tiếp
a Tìm m để phương trình \(x^2-\left(2m+1\right)x+m^2+1=0\)
có hai nghiệm phân biệt trong đó nghiệm này
gấp đôi nghiệm kia
b Tìm m để phương trình \(x^2-2mx+m-3=0\) có hai nghiệm \(x_1,x_2\) thỏa mãn \(x_1+2x_2\) =1
c Tìm m để phương trình \(x^2-2mx+\left(m-1\right)^3=0\)
có hai nghiệm trong đó nghiệm này là bình
phương của nghiệm kia .
d Tìm m để phương trình \(2x^2-\left(m+1\right)x+m+3=0\) có hai nghiệm sao cho hiệu hai nghiệm bằng 1.
d: Ta có: \(\text{Δ}=\left(m+1\right)^2-4\cdot2\cdot\left(m+3\right)\)
\(=m^2+2m+1-8m-24\)
\(=m^2-6m-23\)
\(=m^2-6m+9-32\)
\(=\left(m-3\right)^2-32\)
Để phương trình có hai nghiệm phân biệt thì \(\left(m-3\right)^2>32\)
\(\Leftrightarrow\left[{}\begin{matrix}m-3>4\sqrt{2}\\m-3< -4\sqrt{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m>4\sqrt{2}+3\\m< -4\sqrt{2}+3\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+1}{2}\\x_1x_2=\dfrac{m+3}{2}\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{m+1}{2}\\x_1-x_2=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=\dfrac{m+3}{2}\\x_2=x_1-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+3}{4}\\x_2=\dfrac{m+3}{4}-\dfrac{4}{4}=\dfrac{m-1}{4}\end{matrix}\right.\)
Ta có: \(x_1x_2=\dfrac{m+3}{2}\)
\(\Leftrightarrow\dfrac{\left(m+3\right)\left(m-1\right)}{16}=\dfrac{m+3}{2}\)
\(\Leftrightarrow\left(m+3\right)\left(m-1\right)=8\left(m+3\right)\)
\(\Leftrightarrow\left(m+3\right)\left(m-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-3\\m=9\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Cho phương trình x2 - 2(m - 1)x + 2m - 5 = 0
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m.
b) Tìm m để phương trình có hai nghiệm trái dấu. Khi đó hai nghiệm mang dấu gì?
c) Tìm GTLN của biểu thức A = 4x1x2 - x12 - x22.
Cho phương trình x2 - (m-1)x-2m-1=0 (1) (m là tham số)
a. Tìm m để phương trình (1) vô nghiệm, có nghiệm, có hai nghiệm phân biệt.
b. Tìm m để phương trình (1) có hai nghiệm phân biệt cùng dương.
c. Tìm m để phương trình (1) có hai nghiệm phân biệt x1 x2 thỏa mãn x12 +x22 =3
a:
\(\text{Δ}=\left(m-1\right)^2-4\left(-2m-1\right)\)
\(=m^2-2m+1+8m+4=m^2+6m+5\)
Để (1) vô nghiệm thì (m+1)(m+5)<0
hay -5<m<-1
Để (1) có nghiệm thì (m+1)(m+5)>=0
=>m>=-1 hoặc m<=-5
Để (1) có hai nghiệm phân biệt thì (m+1)(m+5)>0
=>m>-1 hoặc m<-5
b: Để (1) có hai nghiệm phân biệt cùng dương thì
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
Đúng 1
Bình luận (0)
c. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=3\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)
\(\Leftrightarrow\left(m-1\right)^2+2\left(2m+1\right)=3\)
\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\left(loại\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho phương trình x² +(m+3)x-2m+2=0 a. Tìm m để phương trình có hai nghiệm trái dấu. b. Tìm m để phương trình có hai nghiệm dương phân biệt. c. Tìm m để phương trình có hai nghiệm âm phân biệt. d. Tìm m để phương trình có ít một nghiệm dương.
Sửa đề: \(x^2+\left(m+3\right)x+2m+2=0\)
a: Để phương trình có hai nghiệm trái dấu thì 2m+2<0
hay m<-1
b: \(\text{Δ}=\left(m+3\right)^2-4\left(2m+2\right)\)
\(=m^2+6m+9-8m-8\)
\(=m^2-2m+1=\left(m-1\right)^2>=0\)
Do đó: Phương trình luôn có hai nghiệm với mọi m
Để phương trình có hai nghiệm dương phân biệt thì \(\left\{{}\begin{matrix}m-1< >0\\2m+2>0\\m+3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-1\\m< >1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 1:Phương trình √x²-4x+3 -x²+4x-m=0 có hai nghiệm phân biệt
Câu 2: phương trình 6+x+2√(4-x)(2x-2)=m+4(√4-x +√ 2x+2 ) có nghiệm khi
Câu 3. Cho phương trinh x ^ 2 - (2m - 1) * x - 8m = 0(1) ( m là tam số) a) Giải phương trình khi m=1 b) Tim m dễ phương trình có hai nghiệm phân biệt X1, X2 thoả mãn 3x1^2 + 3x2^2 + 2x₁X² = - 5
a: Khi m=1 thì (1) sẽ là:
x^2-x-8=0
=>\(x=\dfrac{1\pm\sqrt{33}}{2}\)
b: 3x1^2+3x2^2+2x1x2=5
=>3[(x1+x2)^2-2x1x2]+2x1x2=5
=>3[(2m-1)^2-2(-8m)]+2(-8m)=5
=>3(4m^2-4m+1+16m)-16m=5
=>12m^2+36m+3-16m-5=0
=>12m^2+20m-2=0
=>\(m=\dfrac{-5\pm\sqrt{31}}{6}\)
Đúng 1
Bình luận (0)


