Cho hình bình hành ABCD tâm I : Có bao nhiêu vecto cùng phương với vecto AI
AT
Những câu hỏi liên quan
Cho hình bình hành ABCD,có tâm O:
a) Tìm điểm I thỏa đẳng thức vecto: IA+IB+IC=BC
b) Gọi M nằm trên cạnh DC sao cho 2DM=MC.Biểu diễn OM theo 2 vecto AB và AD
Cho hình bình hành ABCD có tâm O. CMR
a/ vecto AB+OD+OC=AC
b/ vecto BA+BC+OB=OD
c/ vecto BA+BC=MO-MB-OB
cho hình bình hành ABCD tâm O, M là trung điểm OB
a, chứng minh vecto AB- vecto DA +vecto CD=vecto AD
b, điểm N thuộc BC thỏa mãn vecto BN=k vectoBC , tìm k để A,M,N thẳng hàng
\(a,\overrightarrow{AB}-\overrightarrow{DA}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{0}=\overrightarrow{AD}\)
\(b,\overrightarrow{AM}=\dfrac{\overrightarrow{AO}+\overrightarrow{AB}}{2}=\dfrac{\overrightarrow{AB}}{2}+\dfrac{\dfrac{1}{2}\overrightarrow{AC}}{2}=\overrightarrow{\dfrac{AB}{2}}+\dfrac{1}{4}\overrightarrow{AC}\)
\(=\overrightarrow{\dfrac{AB}{2}}+\dfrac{\overrightarrow{AB}+\overrightarrow{BC}}{4}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{\overrightarrow{BC}}{4}=\dfrac{1}{4}\overrightarrow{BC}+\dfrac{3}{4}\overrightarrow{AB}\left(1\right)\)
\(\overrightarrow{AN}=\overrightarrow{BN}-\overrightarrow{BA}=k.\overrightarrow{BC}+\overrightarrow{AB}\left(2\right)\)
\(\left(1\right)\left(2\right)A,M,N\) \(thẳng\) \(hàng\Leftrightarrow\dfrac{k}{\dfrac{1}{4}}=\dfrac{1}{\dfrac{3}{4}}\Leftrightarrow k=\dfrac{1}{3}\)
Đúng 3
Bình luận (0)
Cho hình bình hành ABCD tâm O chứng minh các vecto BD-BA=OC-OB Giúp mình với ạ
\(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BO}+\overrightarrow{OC}=\overrightarrow{BC}\)(1)
ABCD là hình bình hành
=>\(\overrightarrow{BD}=\overrightarrow{BA}+\overrightarrow{BC}\)
=>\(\overrightarrow{BC}=\overrightarrow{BD}-\overrightarrow{BA}\left(2\right)\)
Từ (1) và (2) suy ra \(\overrightarrow{OC}-\overrightarrow{OB}=\overrightarrow{BD}-\overrightarrow{BA}\)
Đúng 0
Bình luận (0)
Trên hình bình hành abcd tâm o lấy m n sao cho vecto am=vecto mb vectoan=2vectond.gọi k h lần lượt là trung điểm mn oc biểu diễn kh theo vecto ad ab
\(\overrightarrow{AM}=\overrightarrow{MB}=\overrightarrow{MA}+\overrightarrow{AB}=-\overrightarrow{AM}+\overrightarrow{AB}\Rightarrow2\overrightarrow{AM}=\overrightarrow{AB}\Rightarrow\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{AN}=2\overrightarrow{ND}=2\left(\overrightarrow{NA}+\overrightarrow{AD}\right)=-2\overrightarrow{AN}+2\overrightarrow{AD}\Rightarrow3\overrightarrow{AN}=2\overrightarrow{AD}\Rightarrow\overrightarrow{AN}=\dfrac{2}{3}\overrightarrow{AD}\)
Do K là trung điểm MN
\(\Rightarrow\overrightarrow{AK}=\dfrac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\dfrac{1}{2}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AD}\right)=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AD}\)
Theo tính chất hbh: \(\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}\)
Do O là tâm hình bình hành \(\Rightarrow\overrightarrow{AO}=\overrightarrow{OC}=\dfrac{1}{2}\overrightarrow{AC}\)
Mà H là trung điểm OC \(\Rightarrow\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{OC}=\dfrac{1}{4}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AH}=\overrightarrow{AO}+\overrightarrow{OH}=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\)
\(\Rightarrow\overrightarrow{KH}=\overrightarrow{KA}+\overrightarrow{AH}=-\overrightarrow{AK}+\overrightarrow{AH}\)
\(=-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)
Đúng 3
Bình luận (0)
\(\overrightarrow{AN}=2\overrightarrow{ND}\)
=>A,N,D thẳng hàng và AN=2ND
ABCD là hình bình hành tâm O
=>O là trung điểm chung của AC và BD
H là trung điểm của OC
nên HO=HC=1/2CO
=>\(HO=HC=\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot CA=\dfrac{1}{4}CA\)
\(\overrightarrow{AM}=\overrightarrow{MB}\)
=>AM=MB và M nằm giữa A và B
=>M là trung điểm của AB
AN+ND=AD
=>2ND+ND=AD
=>AD=3ND
=>AN/AD=2/3
=>\(\overrightarrow{AN}=\dfrac{2}{3}\cdot\overrightarrow{AD}\)
\(\overrightarrow{KH}=\overrightarrow{KM}+\overrightarrow{MH}\)
\(=\dfrac{1}{2}\overrightarrow{NM}+\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CH}\)
\(=\dfrac{1}{2}\left(\overrightarrow{NA}+\overrightarrow{AM}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{BC}+\dfrac{1}{4}\overrightarrow{CA}\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}+\dfrac{1}{4}\left(\overrightarrow{CD}+\overrightarrow{CB}\right)\)
\(=-\dfrac{1}{3}\overrightarrow{AD}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AD}-\dfrac{1}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{5}{12}\overrightarrow{AD}\)
Đúng 0
Bình luận (0)
Cho lục giác đều ABCDEF tâm O . Hỏi có bao nhiêu vecto khác vecto không ; cùng phương
O
C
→
với có điểm đầu và điểm cuối là các đỉnh của lục giác? A. 3 B. 5 C. 6 D. 8
Đọc tiếp
Cho lục giác đều ABCDEF tâm O . Hỏi có bao nhiêu vecto khác vecto không ; cùng phương O C → với có điểm đầu và điểm cuối là các đỉnh của lục giác?
A. 3
B. 5
C. 6
D. 8
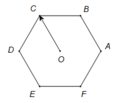
Các vecto cùng phương O C → với có điểm đầu và điểm cuối là các đỉnh của lục giác
![]() : .
: .
Chọn C.
Đúng 0
Bình luận (0)
Cho lục giác đều ABCDEF tâm O . Hỏi có bao nhiêu vecto khác vecto không; cùng phương với O C → có điểm đầu và điểm cuối là các đỉnh của lục giác?
A. 3
B. 5
C. 6
D. 8
Chọn C.
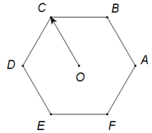
Các vecto cùng phương với ![]() có điểm đầu và điểm cuối là các đỉnh của lục giác :
có điểm đầu và điểm cuối là các đỉnh của lục giác : ![]()
Đúng 0
Bình luận (0)
chọn phát biểu sai trong các phát biểu sau:
A. | vecto AB | = AB
B. trong hình bình hành ABCD ta luôn có: vecto AB + vecto AD = vecto AC
C. Điểm I là trung điểm của đoạn AB khi và chỉ khi IA = IB
D. Với 3 điểm ABC bất kì ta luôn có vecto AB + vecto BC = vecto AC
: Cho hình bình hành ABCD có tâm O. Tìm các vecto sau
a) BD-BA
b)bc-bd+ba
c)oc+ab-do
d)ad-ba-ao
a: \(\overrightarrow{BD}-\overrightarrow{BA}=\overrightarrow{AD}\)
b: \(\overrightarrow{BC}-\overrightarrow{BD}+\overrightarrow{BA}=\overrightarrow{BD}-\overrightarrow{BD}=\overrightarrow{0}\)
Đúng 0
Bình luận (1)
Cho hình bình hành abcd .Tính vecto bc - vecto ab
Do ABCD là hình bình hành
\(\Rightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\overrightarrow{BC}-\overrightarrow{AB}=\overrightarrow{BC}-\overrightarrow{DC}=\overrightarrow{BC}+\overrightarrow{CD}=\overrightarrow{BD}\)
Đúng 0
Bình luận (0)




