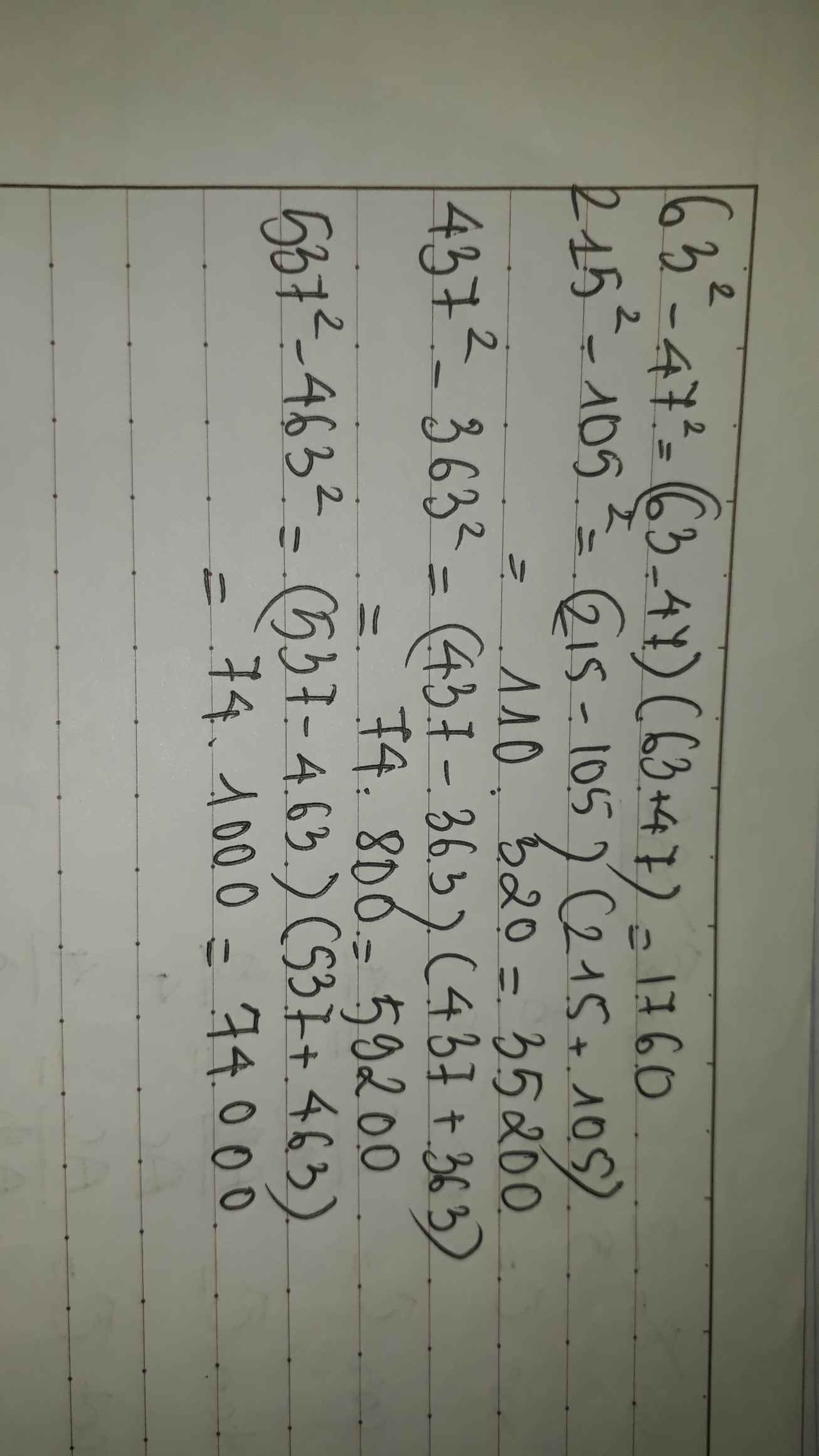tính giá trị biểu thức
\(\frac{437^2-363^2}{537^2-463^2}\)
hãy rút gọn giá trị nếu có thể
VQ
Những câu hỏi liên quan
Bài 1 Tính giá trị của biểu thức
63^2 − 47^2
215^2 − 105^2 ,437^2 − 363^2
537^2 − 463^2
\(63^2-47^2\)
= \(\left(63-47\right)\left(63+47\right)\)
= \(16.110\)
= \(1760\)
Đúng 0
Bình luận (0)
a) \(63^2-47^2=\left(63-47\right)\left(63+47\right)=16\cdot110=1760\)
b) \(215^2-105^2=\left(215-105\right)\left(215+105\right)=35200\)
c) \(437^2-363^2=59200\)
d) \(537^2-463^2=74000\)
Đúng 0
Bình luận (0)
tính giá trị biểu thức:
a) (63^2 - 47^2) / (215^2 - 105^2)
b) (437^2 - 363^2) / (537^2 - 463^2)
Tính giá trị biểu thức sau:
A = \(\frac{63^2-47^2}{215^2-105^2}\)
B = \(\frac{437^2-363^2}{537^2-463^2}\)
\(A=\frac{63^2-47^2}{215^2-105^2}=\frac{\left(63+47\right)\left(63-47\right)}{\left(215+105\right)\left(215-105\right)}=\frac{110\cdot16}{320\cdot110}=\frac{1}{20}\)
\(B=\frac{437^2-363^2}{537^2-463^2}=\frac{\left(473-363\right)\left(473+363\right)}{\left(573-463\right)\left(573+463\right)}=\frac{110\cdot836}{110\cdot1036}=\frac{836}{1036}=\frac{4\cdot209}{4\cdot234}=\frac{209}{234}\)
Đúng 0
Bình luận (0)
Trả lời:
\(A=\frac{63^2-47^2}{215^2-105^2}=\frac{\left(63-47\right).\left(63+47\right)}{\left(215-105\right).\left(215+105\right)}=\frac{16.110}{110.320}=\frac{1}{20}\)
\(B=\frac{437^2-363^2}{537^2-463^2}=\frac{\left(437-363\right).\left(437+363\right)}{\left(537-463\right).\left(537+463\right)}=\frac{74.800}{74.1000}=\frac{4}{5}\)
Học tốt
Áp dụng HĐT số 3 bạn nhé '-'
\(A=\frac{63^2-47^2}{215^2-105^2}=\frac{\left(63+47\right)\left(63-47\right)}{\left(215+105\right)\left(215-105\right)}=\frac{110\cdot16}{320\cdot110}=\frac{16}{320}=\frac{1}{20}\)
\(B=\frac{437^2-363^2}{537^2-463^2}=\frac{\left(437+363\right)\left(437-363\right)}{\left(537+463\right)\left(537-463\right)}=\frac{800\cdot74}{1000\cdot74}=\frac{800}{1000}=\frac{8}{10}=\frac{4}{5}\)
Tính giá trị của biểu thức:
a) \(\frac{63^2-47^2}{215^2-105^2}\)
b) \(\frac{437^2-363^2}{537^2-463^2}\)
Tính
\(\frac{437^2-363^2}{537^2-463^2}\)
\(\frac{437^2-363^2}{537^2-463^2}\)
\(=\frac{\left(437-363\right)\left(437+363\right)}{\left(537-463\right)\left(537+463\right)}\)
\(=\frac{74.800}{74.1000}\)
\(=\frac{80}{1000}=\frac{2}{25}\)
Đúng 0
Bình luận (0)
\(\frac{437^2-363^2}{537^2-463^2}\)
\(=\frac{\left(437-363\right)\left(437+363\right)}{\left(537-463\right)\left(537+463\right)}\)( Áp dụng hằng đẳng thức \(A^2-B^2=\left(A-B\right)\left(A+B\right)\))
\(=\frac{74\cdot800}{74\cdot1000}\)
\(=\frac{4}{5}\)
Đúng 0
Bình luận (0)
Tính giá trị biểu thức 1 cách hợp lý:
\(a.A=\frac{63^2-47^2}{215^2-105^2}\)
\(b,B=\frac{437^2-363^2}{537^2-463^2}\)
\(c,C=\frac{258^2-242^2}{254^2-246^2}\)
\(d.D=263^2+74.263+37^2\)
\(e.E=136^2-92.136+46^2\)
Giúp mk nha!Mk đang cần gấp!
\(\frac{63^2-47^2}{215^2-105^2}=\) \(\frac{\left(63-47\right)\left(63+47\right)}{\left(215-105\right)\left(215+105\right)}\)
\(=\frac{16.110}{110.320}=\frac{16}{320}\)\(=\frac{1}{20}\)
các câu kia làm tương tự nha
Đúng 0
Bình luận (0)
nhưng câu d với câu e mk khô hiểu lắm!
Đúng 0
Bình luận (0)
Rút gọn các biểu thức
A=\(\frac{63^2-47^2}{215^2-105^2}\) B=\(\frac{437^2-363^2}{537^2-463^2}\) C=(2+1)(2\(^2\)+1)(2\(^4\)+1)(2\(^8\)+1)(2\(^{16}\)+1)
A=\(\frac{63^2-47^2}{215^2-105^2}\)
A=\(\frac{\left(63-47\right).\left(63+47\right)}{\left(215-105\right).\left(215+105\right)}\)
A=\(\frac{16.110}{110.320}\)
A=\(\frac{1760}{35200}\)
\(A=\frac{1}{20}\)
B=\(\frac{437^2-363^2}{537^2-463^2}\)
B=\(\frac{\left(437-363\right).\left(437+363\right)}{\left(537-463\right).\left(537+463\right)}\)
B=\(\frac{74.800}{74.1000}\)
B=\(\frac{4}{5}\)
Đúng 0
Bình luận (0)
B1. Chứng minh rằng: số 3599 viết được dưới dạng tích của hai số tự nhiên khác 1.
B2. x+y+z = 0 và xy+yz+xz = 0. Chứng minh x=y=z
B3. Tính giá trị biểu thức:
a) \(\frac{63^2-47^2}{215^2-105^2}\) b) \(\frac{437^2-363^2}{537^2-363^2}\)
B4. So sánh A=262 - 242 và B=272 - 252
B3.
a) =\(\frac{\left(63+47\right).\left(63-47\right)}{\left(215+105\right).\left(215-105\right)}\) b) =\(\frac{\left(437+363\right).\left(437-363\right)}{\left(537+463\right).\left(537-463\right)}\)
=\(\frac{110.16}{320.110}\) =\(\frac{800.74}{1000.74}\)
=\(\frac{1}{20}\) =\(\frac{4}{5}\)
Đúng 0
Bình luận (0)
1. Tính giá trị của các biểu thức:
a, \(\dfrac{63^2-47^2}{215^2-105^2}\)
b, \(\dfrac{437^2-363^2}{537^2-463^2}\)
2. So sánh: A=262-242 và B= 272-252
a) \(\dfrac{63^2-47^2}{215^2-105^2}\)
= \(\dfrac{\left(63-47\right)\left(63+47\right)}{\left(215-105\right)\left(215+105\right)}\)
= \(\dfrac{16.110}{110.320}=\dfrac{16}{320}=\dfrac{1}{20}\)
b) \(\dfrac{437^2-363^2}{537^2-463^2}\)
= \(\dfrac{\left(437-363\right)\left(437+363\right)}{\left(537-463\right)\left(537+463\right)}\)
= \(\dfrac{74.800}{74.1000}=\dfrac{800}{1000}=\dfrac{4}{5}\)
2)
A = \(26^2-24^2=\left(26-24\right)\left(26+24\right)=2.50=100\)
B = \(27^2-25^2=\left(27-25\right)\left(27+25\right)=2.52=104\)
Từ đó suy ra A < B
Đúng 0
Bình luận (0)
1.
\(a.\: \dfrac{63^2-47^2}{215^2-105^2}=\dfrac{\left(63-47\right)\left(63+47\right)}{\left(215-105\right)\left(215+105\right)}\\ =\dfrac{16.110}{110.320}=\dfrac{16}{320}=\dfrac{1}{20}\)
\(b.\dfrac{437^2-363^2}{537^2-463^2}=\dfrac{\left(437-363\right)\left(437+363\right)}{\left(537-463\right)\left(537+463\right)}\\ =\dfrac{74.800}{74.1000}=\dfrac{800}{1000}=\dfrac{4}{5}\)
2.
\(A=26^2-24^2=\left(26-24\right)\left(26+24\right)=2.50=100\)
\(B=27^2-25^2=\left(27-25\right)\left(27+25\right)=2.52=104\)
\(vì\:100< 104\:nên\:26^2-24^2< 27^2-25^2\\ hay\:A< B\)
Đúng 0
Bình luận (0)