Tập nghiệm của phương trình
(x-2019)(x+2020)=0
Tìm các ước nguyên tố của nghiệm phương trình:
\(\frac{x-5}{2020}+\frac{x-6}{2019}-\frac{x-7}{2018}-\frac{x-8}{2017}=0\)
\(PT\Leftrightarrow\left(\frac{x-5}{2020}-1\right)+\left(\frac{x-6}{2019}-1\right)-\left(\frac{x-7}{2018}-1\right)-\left(\frac{x-8}{2017}-1\right)=0\)
\(\Leftrightarrow\left(x-2025\right)\left(\frac{1}{2020}+\frac{1}{2019}-\frac{1}{2018}-\frac{1}{2017}\right)=0\)
Dễ thấy \(\left(\frac{1}{2020}+\frac{1}{2019}-\frac{1}{2018}-\frac{1}{2017}\right)< 0\)
\(\Rightarrow x=2025=5^2.3^4\)
Vậy các ước nguyên tố của nghieemh pt là 3,5
tìm nghiệm của phương trình |x-2019|^2019 +|x-2020|^2020=1
Nhận thấy \(x=\left\{2019;2020\right\}\) là 2 nghiệm của pt đã cho
- Với \(x>2020\Rightarrow\left\{{}\begin{matrix}\left|x-2019\right|^{2019}>1\\\left|x-2020\right|^{2020}>0\end{matrix}\right.\) \(\Rightarrow VT>1>VP\)
\(\Rightarrow\) pt vô nghiệm
- Với \(x< 2019\Rightarrow\left\{{}\begin{matrix}\left|x-2019\right|^{2019}>0\\\left|x-2020\right|^{2020}>1\end{matrix}\right.\) \(\Rightarrow VT>1>VP\)
Pt vô nghiệm
- Với \(2019< x< 2020\Rightarrow\left\{{}\begin{matrix}0< x-2019< 1\\0< 2020-x< 1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left|x-2019\right|^{2019}< x-2019\\\left|2020-x\right|^{2020}< 2020-x\end{matrix}\right.\)
\(\Rightarrow VT< x-2019+2020-x=1\Rightarrow VT< VP\)
Pt vô nghiệm
Vậy pt có đúng 2 nghiệm \(\left[{}\begin{matrix}x=2019\\x=2020\end{matrix}\right.\)
Số giá trị nguyên của tham số m nằm trong khoảng (0.2020) để phương trình x - 1 - 2019 - x = 2020 - m có nghiệm là
A. 2020
B. 2021
C. 2019
D. 2018
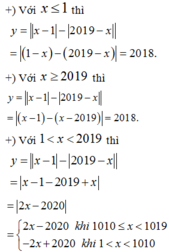
Do đó
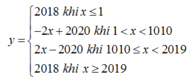
Vẽ dáng đồ thị hàm số ta được:
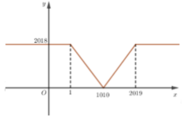
Từ hình vẽ ta thấy phương trình đã cho có nghiệm nếu đường thẳng y = 2020 - m cắt đồ thị hàm số trên tại ít nhất một điểm hay

giá trị của m thỏa mãn bài toán.
Chọn D.
Cho phương trình \(2018x^2-\left(m-2019\right)x-2020=0\) Tìm m để phương trình có hai nghiệm \(x_1;x_2\)thõa mãn
\(\sqrt{x_1^2+2019}-x_2=\sqrt{x_2^2+2019}-x_2\)
srtgb6yyyyyyyy
\(2018x^2-\left(m-2019\right)x-2020=0\)
Ta có \(\Delta=b^2-4ac\)
\(=\left[-\left(m-2019\right)\right]^2-4.2018.\left(-2020\right)\)
\(=\left(m-2019\right)^2+4.2018.2020>0\)( vì \(\left(m-2019\right)^2\ge0\forall x\))
Phương trình có 2 nghiệm \(x_1,x_2\) Áp dụng hệ thức Vi-ét ta có
\(\hept{\begin{cases}x_1+x_2=\frac{m-2019}{2018}\left(1\right)\\x_1.x_2=\frac{-2020}{2018}\left(2\right)\end{cases}}\)
Ta có \(\sqrt{x_1^2+2019}-x_2=\sqrt{x_2^2+2019}-x_2\)
\(\Leftrightarrow\sqrt{x_1^2+2019}-x_2+x_2=\sqrt{x_2^2+2019}\)
\(\Leftrightarrow\sqrt{x_1^2+2019}+0=\sqrt{x_2^2+2019}\)
\(\Leftrightarrow x_1^2+2019=x_2^2+2019\)
\(\Leftrightarrow x_1^2-x_2^2=0\)
\(\Leftrightarrow\left(x_1-x_2\right).\left(x_1+x_2\right)=0\)
\(\Leftrightarrow\left(x_1-x_2\right).\frac{m-2019}{2018}=0\Rightarrow x_1-x_2=0\left(3\right)\)
Thay (3) vào (!) ta có \(\hept{\begin{cases}x_1+x_2=\frac{m-2019}{2018}\\x_1-x_2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}2x_1=\frac{m-2019}{2018}\\x_1-x_2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x_1=\frac{m-2019}{4036}\\x_2=\frac{m-2019}{4036}\end{cases}}\)
\(\Rightarrow x_1.x_2=\frac{-2020}{2018}=\frac{-1010}{1009}\)
\(\Leftrightarrow\frac{m-2019}{4036}.\frac{m-2019}{4036}=\frac{-1010}{1009}\)
\(\Leftrightarrow\frac{\left(m-2019\right)^2}{4036^2}=\frac{-1010}{1009}\)
\(\Leftrightarrow\left(m-2019\right)^2=\frac{4036^2.\left(-1010\right)}{1009}\)
\(\Leftrightarrow\left(m-2019\right)^2=-16305440\left(VL\right)\)
Vậy không có m để thỏa mãn bài toán
Giải phương trình
\(\dfrac{1-\sqrt{x-2019}}{x-2019}+\dfrac{1-\sqrt{y-2020}}{y-2020}+\dfrac{1-\sqrt{z-2021}}{z-2021}+\dfrac{3}{4}=0\)
ĐKXĐ : \(\left\{{}\begin{matrix}x>2019\\y>2020\\z>2021\end{matrix}\right.\)
Đặt \(\sqrt{x-2019}=a,......\)
Ta được PT : \(\dfrac{1-a}{a^2}+\dfrac{1-b}{b^2}+\dfrac{1-c}{c^2}+\dfrac{3}{4}=0\)
\(\Leftrightarrow\dfrac{1}{a^2}-\dfrac{1}{a}+\dfrac{1}{4}+\dfrac{1}{b^2}-\dfrac{1}{b}+\dfrac{1}{4}+\dfrac{1}{c^2}-\dfrac{1}{c}+\dfrac{1}{4}=0\)
\(\Leftrightarrow\left(\dfrac{1}{a}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{b}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{c}-\dfrac{1}{2}\right)^2=0\)
- Thấy : \(\left(\dfrac{1}{a}-\dfrac{1}{2}\right)^2\ge0,......\)
\(\Rightarrow\left(\dfrac{1}{a}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{b}-\dfrac{1}{2}\right)^2+\left(\dfrac{1}{c}-\dfrac{1}{2}\right)^2\ge0\)
- Dấu " = " xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{a}=\dfrac{1}{2}\\\dfrac{1}{b}=\dfrac{1}{2}\\\dfrac{1}{c}=\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=2\\c=2\end{matrix}\right.\)
- Thay lại a. b. c ta được : \(\left\{{}\begin{matrix}\sqrt{x-2019}=2\\\sqrt{y-2020}=2\\\sqrt{z-2021}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2019=4\\y-2020=4\\z-2021=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2023\\y=2024\\z=2025\end{matrix}\right.\) ( TM )
Vậy ...
Giải phương trình x+1/2021+x+2/2020+x+3/2019+x+2028/2=0
=>\(\left(\dfrac{x+1}{2021}+1\right)+\left(\dfrac{x+2}{2020}+1\right)+\left(\dfrac{x+3}{2019}+1\right)+\left(\dfrac{x+2028}{2}-3\right)=0\)
=>x+2022=0
=>x=-2022
Cho phương trình: \(2018x^2-\left(m-2019\right)x-2020=0\) ( m là tham số). Tìm m để phương trình có 2 nghiệm \(x_1,x_2\) thỏa mãn \(\sqrt{x_1^2+2019}-x_1=\sqrt{x_2^2+2019}+x_2\)
PLEASE HELP ME :>
Cho hàm số y= f(x)= ax^2 + bx+c có đồ thị như hình vẽ bên.( dưới bình luận) Có bao nhiêu giá trị nguyên m để phương trình f^2(|x|)+(m- 2019) f (|x|)+m– 2020 =0 có 6 nghiệm phân biệt
Trong các khẳng định sau, số khẳng định đúng là:
a) Tập nghiệm của phương trình x 2 + 3 x x = 0 là {0; 3}
b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0 là {-2}
c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8 là {0}
A. 1
B. 2
C. 0
D. 3