cho tam giác abc vuông tại a có ab=7cm, ac=24 cm tính độ dài đường trung tuyến am
NL
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường trung tuyến AM,BE,CF. Biết AB=6 cm, AC=8 cm. Tính độ dài các đường trung tuyến trong tam giác ABC
Cho tam giác ABC vuông tại A có AB = 8 cm AC = 6 cm độ dài đường trung tuyến AM bằng
A2,5cm
B10cm
C25cm
5cm
Xem thêm câu trả lời
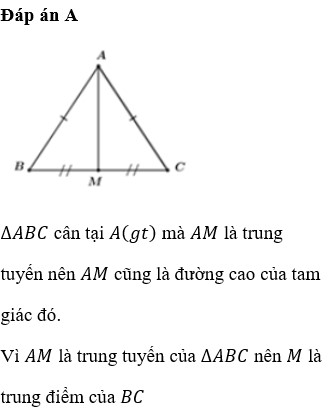
Cho tam giác ABC cân tại A có đường trung tuyến AM.
a) Chứng minh A M ⊥ B C .
b) Biết AB = 10 cm, BC = 12 cm. Tính độ dài đoạn vuông góc kẻ từ B xuống AC.
Cho tam giác ABC cân ở A, đường trung tuyến AM.
a) Chứng minh AM BC
b) Tính AM biết rằng AB cm BC cm 10 , 12
Đúng 0
Bình luận (0)
Câu 1: Cho tam giác ABC có AB = 1 cm, AC = 6 cm. tìm độ dài cạnh BC biết độ dài này là một số nguyên
Câu 2: Cho tam giác ABC vuông tại A, có AB = 3 cm, AC = 4 cm
a/ Tính độ dài BC
b/ Hai đường trung tuyến AM và BN cắt nhau tại G. Tính độ dài AG
Cho tam giác ABC cân tại A, trung tuyến AM. Biết BC=24 cm, AM=5 cm. Tính độ dài các cạnh AB, AC
A. AB=AC=13 cm
B. AB=AC=14 cm
C. AB=AC=15 cm
D. AB=AC=16 cm
Câu 7: cho tam giác ABC vuông tại A, đường cao AH, phân giác AD, trung tuyến AM. Biết ABv= 24 cm, AM = 20 cm. Độ dài AC, BH, HM là
Gấp !!!
Vì `\triangle ABC` vuông tại `A` có `AM` là đường trung tuyến
`=>AM=MC=1/2BC =>BC =40(cm)`
`@` Xét `\triangle ABC` vuông tại `A` có: `AC=\sqrt{BC^2 -AB^2}=32(cm)` (Py-ta-go)
`@` Mặt khác: Ta có `AH` là đường cao
`=>BH=[AB^2]/[BC]` (Ht giữa cạnh và đường cao)
`=>BH =14,4(cm)`
`@` Ta có: `HM =BC-BH-MC=5,6(cm)`
Đúng 2
Bình luận (0)
Cho tam giác ABC có BC= 1cm; AC= 7cm và độ dài cạnh AB là một số nguyên (cm).Tính độ dài AB và cho biết tam giác ABC là tam giác gì?
A. AB= 7cm và tam giác ABC vuông tại A
B. AB= 7cm và tam giác ABC cân tại A
C. AB= 7cm và tam giác ABC vuông cân tại A
D. AB= 8cm và tam giác ABC vuông tại B
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, có AB = 15cm và AC = 20cm. Tính độ dài đường cao AH và trung tuyến AM của tam giác ABC.
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=12\left(cm\right)\)
Do AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{25}{2}=12,5\left(cm\right)\)
Đúng 1
Bình luận (0)
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=225+400=625\Rightarrow BC=25\)cm
Xét tam giác ABC, đường cao AH
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{300}{25}=12\)cm
Vì AM là đường trung tuyến suy ra : \(AM=\dfrac{BC}{2}=\dfrac{25}{2}\)cm
Đúng 1
Bình luận (0)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=15^2+20^2=625\)
hay BC=25(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot25=15\cdot20=300\)
hay AH=12(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(gt)
nên \(AM=\dfrac{BC}{2}=\dfrac{25}{2}=12.5\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A , đường cao AH , trung tuyến AM .Biết AH =4 cm , AM = 4,1 cm . Tỉ số độ dài 2 canh goc vuông AB và AC của tam giác ABC = ?