\(2x^2-6x-3=0\)

\(\Delta'=\left(-3\right)^2+3.2=15>0\)

⇒ Phương trình có hai nghiệm phân biệt với mọi m.

Theo hệ thức viét ta có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1.x_2=-\dfrac{3}{2}\end{matrix}\right.\)

Ta có : \(B=3x_1x_2-x_1^2-x_2^2=-\left(x_1+x_2\right)^2+5x_1x_2=-9+5.\left(-\dfrac{3}{2}\right)=\dfrac{135}{2}\)

Vậy \(B=-\dfrac{135}{2}\) với hai nghiệm phân biệt thỏa mãn.

\(2x^2-6x-3=0\)

\(\Delta'=3^2+3.2=15>0\)

⇒ Phương trình có hai nghiệm phân biệt.

Theo hệ thức viét có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\)

Ta có : \(A=x_1^2x_2^2-2x_1-2x_2=\left(x_1x_2\right)^2-2\left(x_1+x_2\right)=\left(-\dfrac{3}{2}\right)^2-2.3=-\dfrac{15}{4}\)

Vậy \(A=-\dfrac{15}{4}\) thì thỏa mãn điều kiện bài ra.

Áp dụng hệ thức Vi-et, ta được:

\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{6}{2}=-3\\x_1x_2=\dfrac{-3}{2}\end{matrix}\right.\)

Ta có: \(\dfrac{2}{x_1^2}+\dfrac{2}{x_2^2}\)

\(=\dfrac{2x^2_2+2x_1^2}{\left(x_1\cdot x_2\right)^2}\)

\(=\dfrac{2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]}{\left(-\dfrac{3}{2}\right)^2}=\dfrac{2\cdot\left[\left(-3\right)^2-2\cdot\dfrac{-3}{2}\right]}{\dfrac{9}{4}}\)

\(=\dfrac{2\cdot12}{\dfrac{9}{4}}=24\cdot\dfrac{4}{9}=\dfrac{96}{9}=\dfrac{32}{3}\)

TK

Điều kiện xác định: x ≠ 3.

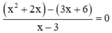
Suy ra: (x2 + 2x) – (3x + 6) = 0

⇔ x(x + 2) – 3(x + 2) = 0

⇔ (x – 3)(x + 2) = 0

⇔ x – 3 = 0 hoặc x + 2 = 0

+ x – 3 = 0 ⇔ x = 3 (Không thỏa mãn đkxđ)

+ x + 2 = 0 ⇔ x = -2 (Thỏa mãn đkxđ).

Vậy phương trình có tập nghiệm S = {-2}.

Ta có:  - 2   x 2  + 6x = 0 ⇔ x(6 -  2  x) = 0

⇔ x = 0 hoặc 6 -  2  x = 0 ⇔ x = 0 hoặc x = 3 2

Vậy phương trình có hai nghiệm x 1  = 0,  x 2  = 3 2

Theo vi ét: \(\left\{{}\begin{matrix}x_1+x_2=6\\x_1x_2=8\end{matrix}\right.\)

Theo đề:

\(B=\dfrac{x_1\sqrt{x_1}-x_2\sqrt{x_2}}{x_1-x_2}=\dfrac{\left(\sqrt{x_1}-\sqrt{x_2}\right)\left(x_1+\sqrt{x_1x_2}+x_2\right)}{\left(\sqrt{x_1}-\sqrt{x_2}\right)\left(\sqrt{x_1}+\sqrt{x_2}\right)}\left(x_1,x_2\ge0\right)\)

\(=\dfrac{6+\sqrt{8}}{\sqrt{x_1}+\sqrt{x_2}}\)

Tính: \(\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=x_1+x_2+2\sqrt{x_1x_2}=6+2\sqrt{8}=6+4\sqrt{2}=\left(\sqrt{4}+\sqrt{2}\right)^2\)

\(\Rightarrow\sqrt{x_1}+\sqrt{x_2}=\sqrt{4}+\sqrt{2}\) (thỏa mãn \(x_1,x_2\ge0\))

Khi đó: \(P=\dfrac{6+\sqrt{8}}{\sqrt{4}+\sqrt{2}}=4-\sqrt{2}\)