LD
Những câu hỏi liên quan
Trong mpOxy, cho tam giác ABC có A(1; 1), B(3; 3), C(0;-6).
1,Tính cos A.
2,Tìm tọa độ điểm D sao cho tam giác ABD vuông cân tại D.
3,Gọi E là chân đường phân giác trong của góc A.Tìm tọa độ điểm E.
Trong mpOxy ,cho các điểm A(1.-2),B(0,4), C(3,2).Tìm tọa độ điểm M thỏa hệ thức vecto CM=2 vectoAB-4 vectoAC
Bài 1: Trong mpOxy cho tam giác ABC với A(0;1) B(3;2) và C(1;5). Tìm trực tâm H của tam giác ABC .
Bài 2: Trong mpOxy cho tam giác ABC với A(1;5) B(–4;–5) và C(4;-1). Tìm tâm J của đường tròn nội tiếp tam giác ABC.
Bài 3: Trong mpOxy cho tam giác ABC với A(1 ; 5) B(3;–1) C(6;0). Tìm chân đường cao B’ kẻ từ B lên CA.
Bài 1: Trong mpOxy cho tam giác ABC với A(3;–1) B(1;5) và C(6;0) . Gọi A’ là chân đường cao kẻ từ A lên BC tìm A’.
Bài 2: Trong mpOxy cho tam giác ABC với A(0;3) B(2;2) và C(–6;1). Tính số đo của góc A.
Bài 6. Trong mpOxy, cho A(−2;6), B(1;2) , C(9;8). a) Chứng minh tam giác ABC vuông. b) Gọi I là trung điểm của cạnh AC. Tìm tọa độ trực tâm H của tam giác ABI. c) Tìm tọa độ điểm E đối xứng với I qua cạnh BC.
Trong mpOxy cho A(3;0) và đường thẳng \(\left(\Delta\right):\frac{x=2+t}{y=3+2t}\)
a) Tìm điểm B đối xứng của A qua \(\left(\Delta\right)\)
b) viết phương trình đường thẳng delta' là đối xứng của \(\left(\Delta\right)\) qua A
\(\left\{{}\begin{matrix}t=x-2\\t=\frac{y-3}{2}\end{matrix}\right.\) \(\Rightarrow x-2=\frac{y-3}{2}\Leftrightarrow2x-y-1=0\)
Gọi d là đường thẳng qua A và vuông góc \(\Delta\Rightarrow\) d nhận \(\left(1;2\right)\) là 1 vtpt
Phương trình d: \(1\left(x-3\right)+2y=0\Leftrightarrow x+2y-3=0\)
Gọi C là giao điểm d và \(\Delta\Rightarrow\) tọa độ C thỏa: \(\left\{{}\begin{matrix}2x-y-1=0\\x+2y-3=0\end{matrix}\right.\) \(\Rightarrow C\left(1;1\right)\)
B đối xứng A qua \(\Delta\Leftrightarrow C\) là trung điểm AB
\(\Rightarrow\left\{{}\begin{matrix}x_B=2x_C-x_A=-1\\y_B=2y_C-y_A=2\end{matrix}\right.\) \(\Rightarrow B\left(-1;2\right)\)
\(\Delta'\) đối xứng \(\Delta\) qua A \(\Rightarrow\Delta'//\Delta\) và đi qua B
\(\Rightarrow\Delta'\) nhận \(\left(2;-1\right)\) là 1 vtpt và qua B
Pt \(\Delta'\): \(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho các điểm
A
0
;
4
2
;
0
,
B
0
,
0
,
4
2
điểm
C
∈
m
p
O
x
y...
Đọc tiếp
Trong không gian Oxyz, cho các điểm A 0 ; 4 2 ; 0 , B 0 , 0 , 4 2 điểm C ∈ m p O x y và tam giác OAC vuông tại C; hình chiếu vuông góc của O trên BC là điểm H. Khi đó điểm H luôn thuộc đường tròn cố định có bán kính bằng:
A. 2 2
B. 4
C. 3
D. 2
Ta có:
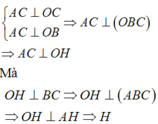
di động trên mặt cầu đường kính OA.
Mặt khác O H ⊥ B H ⇒ H di động trên mặt cầu đường kính OB.
⇒ H di động trên đường tròn cố định là giao tuyến của hai mặt cầu trên (mặt cầu đường kính OA và mặt cầu đường kính OB)
Bán kính cần tìm là:
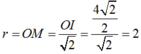
(do tam giác OIM vuông cân tại M)
Chọn D.
Đúng 0
Bình luận (0)
Trong mpOxy, cho HBH ABCD có phương trình đường chéo AC:x-y+1=0, điểm G(1;4) là trọng tâm tam giác ABC,điểm E(0;3) thuộc đường cao kẻ từ D của tam giác ACD.Tìm tọa độ các đỉnh HBH biết diện tích tứ giác AGCD bằng 32 và đỉnh A có tung độ dương.
bạn thử kiểm tra lại đề xem có fải sai đề k
Đúng 0
Bình luận (0)
Bài 1 . Trong mpoxy, cho (P):y1/2x^2 và (d) y (2m-1)x +5
a) vẽ (p)
b) Tìm m để (d) đi qua điểm E(7;12)
c) Đường thẳng y2 cắt (P) tại 2 điểm A,B. Tìm tọa độ giao điểm của A,B
Bài 2
a) rút gọn
B(x.sqrt{ }x/sqrt{ }x-1 -sqrt{ }x+1/x+sqrt{ }x) : sqrt{ }x+1/sqrt{ }x
b) Tính giá trị của B khi x12+8sqrt{ }2
Đọc tiếp
Bài 1 . Trong mpoxy, cho (P):y=1/2x^2 và (d) y =(2m-1)x +5
a) vẽ (p)
b) Tìm m để (d) đi qua điểm E(7;12)
c) Đường thẳng y=2 cắt (P) tại 2 điểm A,B. Tìm tọa độ giao điểm của A,B
Bài 2
a) rút gọn
B=(x.\(\sqrt{ }\)x/\(\sqrt{ }\)x-1 -\(\sqrt{ }\)x+1/x+\(\sqrt{ }\)x) : \(\sqrt{ }\)x+1/\(\sqrt{ }\)x
b) Tính giá trị của B khi x=12+8\(\sqrt{ }\)2

