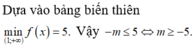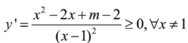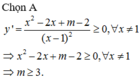Tìm tất cả các giá trị của tham số m để bpt -x2+2x-5/ x2-mx+1</ 0 nghiệm đúng với mọi x thuộc R
TA
Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để hàm số
y
x
2
+
m
x
+
x
-
2
x
-
1
đồng biến trên khoảng
(
1
;
+
∞
)
A.
m
≤
5
B.
m
≤
-...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hàm số y = x 2 + m x + x - 2 x - 1 đồng biến trên khoảng ( 1 ; + ∞ )
A. m ≤ 5
B. m ≤ - 5
C. m ≥ 5
D. m ≥ - 5
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
2
-
m
x
+
2
x
-
1
đồng biến tr...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 2 - m x + 2 x - 1 đồng biến trên từng khoảng xác định của nó.
A.![]()
B. m < 3
C. ![]()
D. ![]() hoặc
hoặc ![]()
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
2
-
m
x
+
2
x
-
1
đồng biến trên từng khoảng xác định của nó A.
m
≥
3
B. m 3 C.
-
2
2...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 2 - m x + 2 x - 1 đồng biến trên từng khoảng xác định của nó
A. m ≥ 3
B. m < 3
C. - 2 2 ≤ m ≤ 2 2
D. m < - 2 2 hoặc m > 2 2
Tìm tất cả các giá trị thực của tham số m để bpt (m+1)x2 -2(m+1)x+4 ≥ 0 có tập nghiệm S=R
Trường hợp 1: m=-1
Bất phương trình sẽ là \(0x^2-2\cdot0\cdot x+4>=0\)(luôn đúng)
Trường hợp 2: m<>-1
\(\text{Δ}=\left(2m+2\right)^2-4\cdot4\cdot\left(m+1\right)\)
\(=4m^2+8m+4-16m-16\)
\(=4m^2-8m-12\)
\(=4\left(m^2-2m-3\right)\)
Để bất phương trình có nghiệm đúng với mọi x thực thì \(\left\{{}\begin{matrix}\left(m-3\right)\left(m+1\right)< 0\\\left(m+1\right)>=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-1< m< 3\\m>=-1\end{matrix}\right.\Leftrightarrow-1< m< 3\)
Vậy: -1<=m<3
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để phương trình
2
(
x
2
+
m
x
)
-
2
(
2
x
2
+
2
m
x
+
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 ( x 2 + m x ) - 2 ( 2 x 2 + 2 m x + m ) = x 2 +mx+m có nghiệm thực
A. ( - ∞ ; 0 ] ∪ [ 1 ; + ∞ ) .
B. ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ ) .
C. ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ ) .
D. ( - ∞ ; - 4 ] ∪ [ 0 ; + ∞ ) .
Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số
y
m
x
-
2
x
-
m
+
1
tiếp xúc với parabol
y
x
2...
Đọc tiếp
Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số y = m x - 2 x - m + 1 tiếp xúc với parabol y = x 2 + 5
A. Không có giá trị m
B.m=5
C.m=6
D. Với mọi ![]()
Đáp án B
Để ![]() có tiệm cận ngang thì
có tiệm cận ngang thì
![]()
Khi đó phương trình đường tiệm cận ngang là ![]()
d tiếp xúc với parabol ![]()
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số
y
m
x
-
2
x
-
m
+
1
tiếp xúc với parabol
y
x
2
+
5
A. Không có giá trị m B. m 5 C. m 6 D. Với mọi mÎR
Đọc tiếp
Tìm tất cả các giá trị của tham số m sao cho tiệm cận ngang của đồ thị hàm số y = m x - 2 x - m + 1 tiếp xúc với parabol y = x 2 + 5
A. Không có giá trị m
B. m = 5
C. m = 6
D. Với mọi mÎR
Tìm tất cả các giá trị thực của tham số m để hàm số
y
x
3
+
x
2
+
m
x
+
1
đồng biến trên
−
∞
;
+
∞
A.
m
≤
4
3
B.
m
≤
1...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hàm số y = x 3 + x 2 + m x + 1 đồng biến trên − ∞ ; + ∞
A. m ≤ 4 3
B. m ≤ 1 3
C. m ≥ 1 3
D. m ≥ 4 3
Tìm tất cả các giá trị thực của tham số m sao cho phương trình
x
2
+
m
x
+
2
2
x
+
1
có hai nghiệm thực? A.
m
≤
3
B.
m
≤
5
C. m1 D. đáp án khác
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho phương trình x 2 + m x + 2 = 2 x + 1 có hai nghiệm thực?
A. m ≤ 3
B. m ≤ 5
C. m>1
D. đáp án khác
Điều kiện: x≥ -1/2
Phương trình
x 2 + m x + 2 = 2 x + 1 ⇔ 3 x 2 + 4 x - 1 = m x ( * )
Vì x= 0 không là nghiệm nên (*)
⇔ m = 3 x 2 + 4 x - 1 x
xét f ( x ) = 3 x 2 + 4 x - 1 x .
Ta có đạo hàm
f ' ( x ) = 3 x 2 + 1 x 2 > 0 ∀ x ⩾ - 1 2 ; x ≠ 0
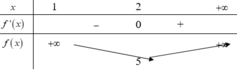
Bảng biến thiên
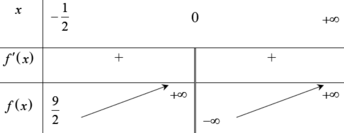
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì m ≥ 9/2.
Chọn D.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho phương trình
x
2
+
m
x
+
2
2
x
+
1
có hai nghiệm thực? A.
m
≥
-
7
2
B.
m
≥
3
2
C.
m
≥...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho phương trình x 2 + m x + 2 = 2 x + 1 có hai nghiệm thực?
A. m ≥ - 7 2
B. m ≥ 3 2
C. m ≥ 9 2
D. với mọi m
Điều kiện: x ≥ - 1 2
Phương trình x 2 + m x + 2 = 2 x + 1 ⇔ 3 x 2 + 4 x - 1 = m x ( * )
Vì x=0 không là nghiệm nên (*) ⇔ m = 3 x 2 + 4 x - 1 x
Xét
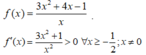
Bảng biến thiên
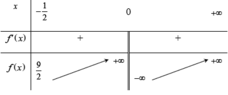
Từ bảng biến thiên ta có để phương trình có hai nghiệm thì m ≥ 9 2 .
Chọn C.
Đúng 0
Bình luận (0)