sin²10º + sin²20º + sin²30º +…+ sin²70º + sin²80º.
Em xin đáp án ạ TvT Cảm ơn mọi người nhiều
Giải phương trình: \(sin^2x+\frac{sin^23x}{3sin3x}\left(cos3xsin^3x+sin3xcos^3x\right)=sinxsin^23x\)
Em cảm ơn mọi người nhiều ạ !
Cho em hỏi: sin(6πt) + cos(5πt) bằng gì ạ ( không phải là ra đáp án số )
Em cảm ơn ạ.
CMR sin2A-sin2B-sin2C = -2cosAsinBsinC
Em cảm ơn nhiều ạ
a) sin^2 . 1° + sin^2 . 2° + sin^2 . 3° + ..... + sin^2 . 89° = ?? , tính
b) cho : sin x + cos x = 7/5 ( 0° < x < 90° ) .. Tính tan x = ?
Mọi người làm giúp em với , em cảm ơn
a) Ta có: \(\sin^2a^o=\cos^2\left(90^o-a^o\right)\)
Biểu thức trên
\(=\left(\sin^21^o+\sin^o89\right)+\left(\sin^22^o+\sin^288^o\right)+...+\left(\sin^244^o+\sin^246^o\right)+\sin^245^o\)
\(=\left(\sin^21^o+\cos^21^o\right)+\left(\sin^22^o+\cos^22^o\right)+...+\left(\sin^244^o+\cos^246^o\right)+\sin^245^o\)
\(=1+1+..+1+\sin^245^o=44+\frac{1}{2}=\frac{89}{2}\)
b)
Ta có: \(\sin^2x+\cos^2x=1\)
\(0^o< x< 90^o\)
=> \(0< \sin x;\cos x< 1\)
Ta có: \(\frac{\sin^2x+\cos^2x}{\text{}\text{}\sin x.\cos x}=\frac{1}{\frac{12}{25}}=\frac{25}{12}\Leftrightarrow\frac{\sin x}{\cos x}+\frac{\cos x}{\sin x}=\frac{25}{12}\)
\(\Leftrightarrow\tan x+\frac{1}{\tan x}=\frac{25}{12}\Leftrightarrow\tan^2x-\frac{25}{12}\tan x+1=0\)
Đặt t =tan x => có phương trình bậc 2 ẩn t => Giải đen ta => ra đc t => ra đc tan t
\(\Leftrightarrow\orbr{\begin{cases}\tan x=\frac{3}{4}\\\tan x=\frac{4}{3}\end{cases}}\)
Giải phương trình:
\(\tan^2x+\cot^2x=2\left(\cos^4x+\sin^4x\right)+\sin^22x\)
Mọi người giúp mình với ạ!! Cảm ơn mọi người nhiều!!
ĐKXĐ: ...
\(\Leftrightarrow tan^2x+cot^2x=2\left(cos^4x+sin^4x+2sin^2x.cos^2x\right)\)
\(\Leftrightarrow tan^2x+cot^2x=2\left(sin^2x+cos^2x\right)^2\)
\(\Leftrightarrow tan^2x+cot^2x=2\)
\(\Leftrightarrow\left(tanx-cotx\right)^2=0\)
\(\Leftrightarrow tanx=cotx=tan\left(\frac{\pi}{2}-x\right)\)
\(\Leftrightarrow x=\frac{\pi}{2}-x+k\pi\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)
Cho tam giác abc vuông ở a chứng tỏ sin b < cot c
xin cảm ơn mọi người nhiều nhiều ạ
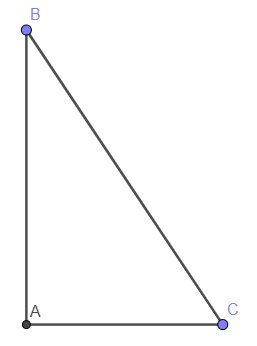
Xét \(\Delta ABC\) vuông tại A có:
\(sin\left(B\right)=\dfrac{AC}{BC}\)
\(cotg\left(C\right)=\dfrac{AC}{AB}\)
BC là cạnh huyền của \(\Delta ABC\) \(\left(AB,AC< BC\right)\)
\(\Rightarrow\dfrac{AC}{BC}< \dfrac{AC}{AB}\Rightarrow sin\left(B\right)< cotg\left(C\right)\)
Tìm GTLN, GTNN của:
a, \(f\left(x\right)=3\sin^2x-2\)
b, \(g\left(x\right)=\sin^2x+3\cos x-2\)
Mọi người giúp em với ạ!!! Em cảm ơn nhiều!!!
a/
\(0\le sin^2x\le1\Rightarrow-2\le f\left(x\right)\le1\)
\(f\left(x\right)_{min}=-2\) khi \(sin^2x=1\)
\(f\left(x\right)_{max}=1\) khi \(sin^2x=1\)
b/
\(g\left(x\right)=1-cos^2x+3cosx-2=-cos^2x+3cosx-1\)
\(=-cos^2x+3cosx-2+1=\left(cosx-1\right)\left(2-cosx\right)+1\)
Do \(-1\le cosx\le1\Rightarrow\left\{{}\begin{matrix}cosx-1\le0\\2-cosx>0\end{matrix}\right.\)
\(\Rightarrow\left(cosx-1\right)\left(2-cosx\right)\le0\Rightarrow g\left(x\right)\le1\)
\(g\left(x\right)_{max}=1\) khi \(cosx=1\)
\(g\left(x\right)=-cos^2x+3cosx+4-5=\left(cosx+1\right)\left(4-cosx\right)-5\)
\(\left(cosx+1\right)\left(4-cosx\right)\ge0\Rightarrow g\left(x\right)\ge-5\)
\(g\left(x\right)_{min}=-5\) khi \(cosx=-1\)
Tìm GTNN, GTLN của hàm số:
\(y=2\sin x+\sqrt{3-\sin^2x}\)
Mọi người giúp mình với ạ!!! Mình cảm ơn nhiều!!!
Ta có: \(sin^2x\le1\Rightarrow y\ge2sinx+\sqrt{3-1}=2sinx+\sqrt{2}\)
Mặt khác \(sinx\ge-1\Rightarrow y\ge-2+\sqrt{2}\)
\(\Rightarrow y_{min}=-2+\sqrt{2}\) khi \(sinx=-1\)
\(y^2=3sin^2x+3+4sinx\sqrt{3-sin^2x}\)
\(y^2=3sin^2x+3+2\sqrt{2}\left(\sqrt{2}sinx.\sqrt{3-sin^2x}\right)\)
\(y^2\le3sin^2x+3+\sqrt{2}\left(2sin^2x+3-sin^2x\right)=\left(3+\sqrt{2}\right)sin^2x+3+3\sqrt{2}\)
Do \(sin^2x\le1\Rightarrow y^2\le3+\sqrt{2}+3+3\sqrt{2}=6+4\sqrt{2}\)
\(\Rightarrow y\le\sqrt{6+4\sqrt{2}}=2+\sqrt{2}\)
\(y_{max}=2+\sqrt{2}\) khi \(sinx=1\)
cho tam giac ABC, xác định GTLN của sin A + sin B - sin C . XIN CẢM ƠN