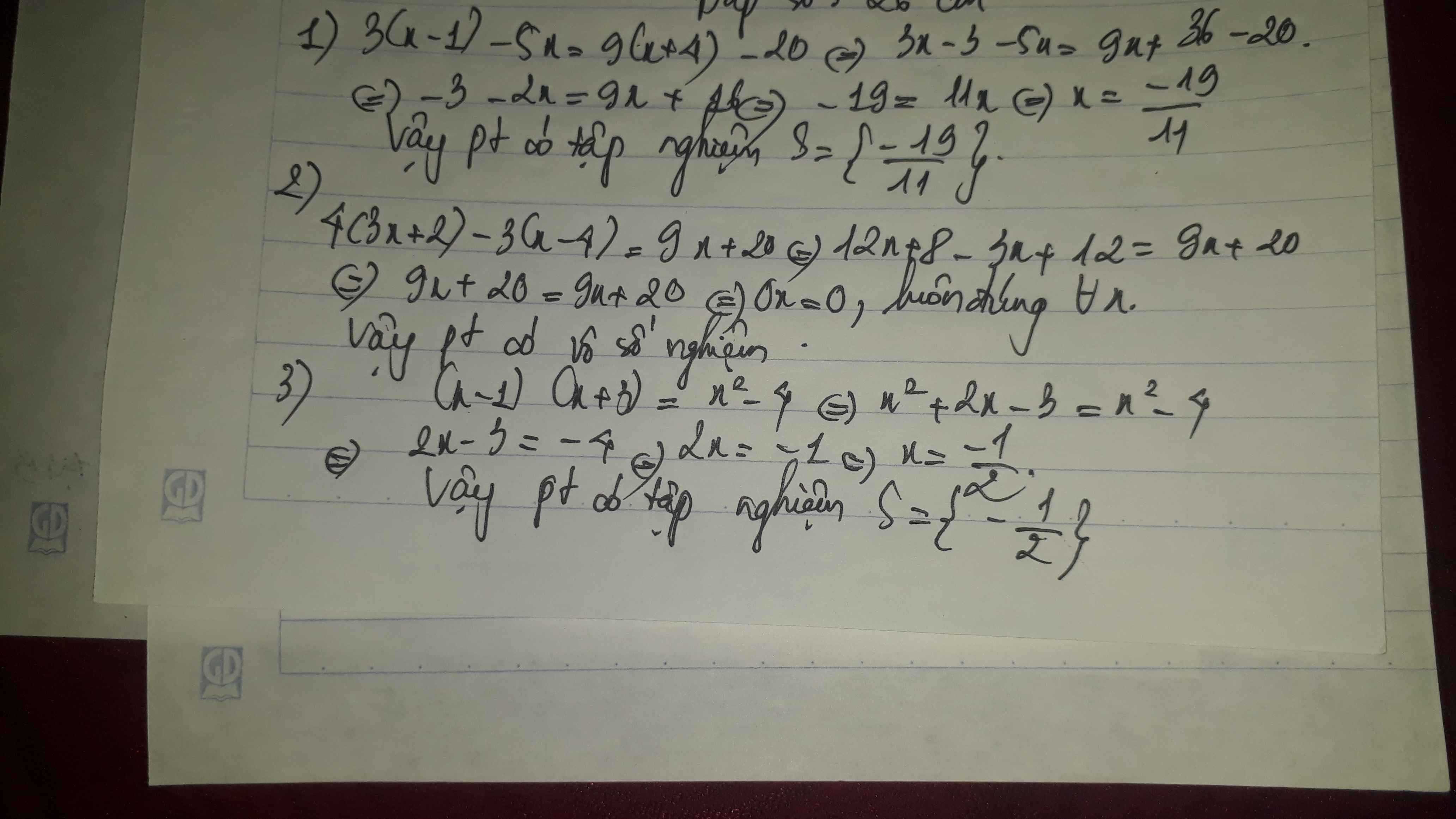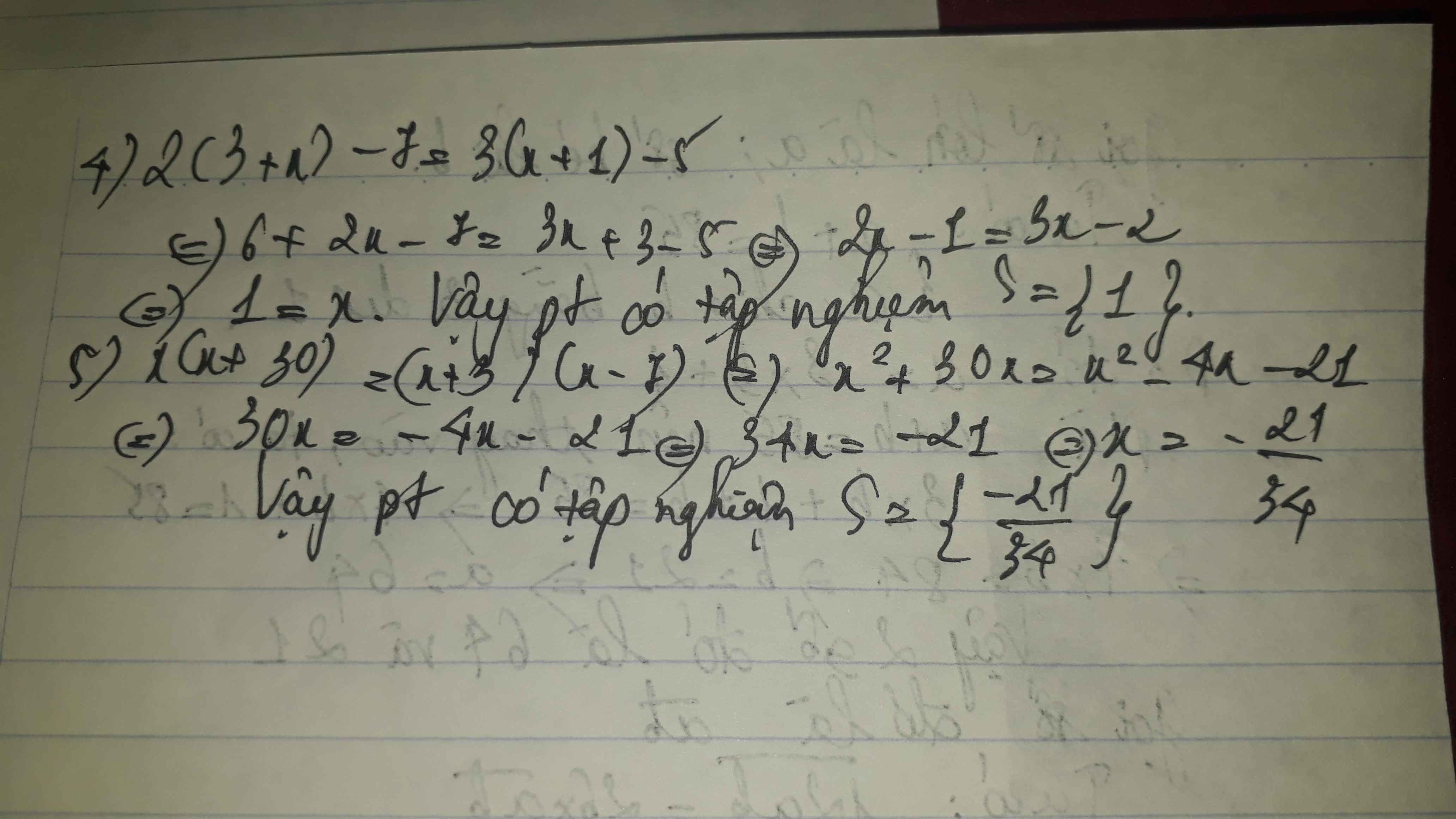dẽ qua ak nhưng giúp mình làm bài này đi

cho tam giac abc . co canh bc=12cm, duong cao ah=8cm

a> tinh s tam giac abc

b> tren canh bc lay diem e sao cho be=3/4bc. tinh s tam giac abe va s tam giac ace ( bằng nhiều cách

c> lay diem chinh giua cua canh ac va m . tinh s tam giac ame

\(\frac{x+1}{58}+\frac{x+2}{57}=\frac{x+3}{56}+\frac{x+4}{55}\)

\(\Rightarrow\left(\frac{x+1}{58}+1\right)+\left(\frac{x+2}{57}+1\right)=\left(\frac{x+3}{56}+1\right)+\left(\frac{x+4}{55}+1\right)\)

\(\Rightarrow\frac{x+59}{58}+\frac{x+59}{57}=\frac{x+59}{56}+\frac{x+59}{55}\)

\(\Rightarrow\frac{x+59}{58}+\frac{x+59}{57}-\frac{x+59}{56}-\frac{x+59}{55}=0\)

\(\Rightarrow\left(x+59\right)\left(\frac{1}{58}+\frac{1}{57}-\frac{1}{56}-\frac{1}{55}\right)=0\)

Mà \(\frac{1}{58}+\frac{1}{57}-\frac{1}{56}-\frac{1}{55}\ne0\)

\(\Rightarrow x+59=0\)

\(\Rightarrow x=-59\)

\(\frac{x+1}{58}+\frac{x+2}{57}=\frac{x+3}{56}+\frac{x+4}{55}\)
\(\Rightarrow\frac{x+59}{58}+\frac{x+59}{57}-\frac{x+59}{56}-\frac{x+59}{55}=0\)
\(\Rightarrow\left(x+59\right)\left(\frac{1}{58}+\frac{1}{57}-\frac{1}{56}-\frac{1}{55}\right)=0\)
Do \(\frac{1}{58}+\frac{1}{57}-\frac{1}{56}-\frac{1}{55}\ne0\) nên \(x+59=0\Rightarrow x=-59\)

1) Ta có: \(3\left(x-1\right)-5x=9\left(x+4\right)-20\)

\(\Leftrightarrow-2x-3=9x+16\)

\(\Leftrightarrow-11x=19\)

hay \(x=-\dfrac{19}{11}\)

2: Ta có: \(4\left(3x+2\right)-3\left(x-4\right)=9x+20\)

\(\Leftrightarrow12x+8-3x+12-9x-20=0\)

\(\Leftrightarrow0x=0\)(luôn đúng

\(\dfrac{x-45}{55}+\dfrac{x-47}{53}=\dfrac{x-55}{45}+\dfrac{x-53}{47}\)

\(\Leftrightarrow\left(\dfrac{x-45}{55}-1\right)+\left(\dfrac{x-47}{53}-1\right)=\left(\dfrac{x-55}{45}-1\right)+\left(\dfrac{x-53}{47}-1\right)\)

\(\Leftrightarrow\dfrac{x-100}{55}+\dfrac{x-100}{53}=\dfrac{x-100}{45}+\dfrac{x-100}{47}\)

\(\Leftrightarrow\dfrac{x-100}{55}+\dfrac{x-100}{53}-\dfrac{x-100}{45}-\dfrac{x-100}{47}=0\)

\(\Leftrightarrow\left(x-100\right)\left(\dfrac{1}{55}+\dfrac{1}{53}-\dfrac{1}{45}-\dfrac{1}{47}\right)=0\)

Do \(\dfrac{1}{55}+\dfrac{1}{53}-\dfrac{1}{45}-\dfrac{1}{47}\ne0\) nên x - 100 = 0 <=> x = 100

=> (x + 1)(x + 5)(x + 2)(x + 4) - 40 = 0

=> (x² + 6x + 5)(x² + 6x + 8) - 40 = 0

Đặt x² + 6x + 5 = a (a > 0)

=> a.(a + 3) - 40 = 0

=> a² + 3a - 40 = 0

=> (a - 5)(a + 8) = 0

=> a = 5 (nhận) hoặc a = -8 (loại)

a = 5 => x² + 6x + 5 = 5 => x² + 6x = 0 => x(x + 6) = 0 => x = 0 hoặc x = -6

Vậy x = 0 , x = -6

x=0

x=0

x=4 hoặc -6

có cần chi tiết ko

<=>\(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)-40=x\left(x+6\right)\left(x^2+6x+13\right)\)

=>x=0 và x=-6

=>\(x^2+6x+13=0\)

=> có biệt thức \(6^2-4\left(1.13\right)=-16\)

=>PT ko có nghiệm thực

=>x=-6 hoặc 0

a) \(x^2+2x=\left(x-2\right).3x\)

\(\Leftrightarrow x^2+2x=3x^2-6x\)

\(\Leftrightarrow x^2+2x-3x^2+6x=0\)

\(\Leftrightarrow-2x^2+8x=0\)

\(\Leftrightarrow-2x\left(x-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

Vậy S = {0;4}

b) \(x^3+x^2-x-1=0\)

\(\Leftrightarrow x^2\left(x+1\right)-\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x^2-1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\mp1\end{matrix}\right.\)

Vậy: S = {-1; 1}

c) \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)

\(\Leftrightarrow\left[\left(x+1\right)\left(x+5\right)\right]\left[\left(x+2\right)\left(x+4\right)\right]=40\)

\(\Leftrightarrow\left(x^2+5x+x+5\right)\left(x^2+4x+2x+8\right)=40\)

\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)=40\)

Đặt x² + 6x + 5 = t

\(\Leftrightarrow t.\left(t+3\right)=40\)

\(\Leftrightarrow t^2+3t=40\)

\(\Leftrightarrow t^2+2.t.\dfrac{3}{2}+\dfrac{9}{4}=\dfrac{169}{4}\)

\(\Leftrightarrow\left(t+\dfrac{3}{2}\right)^2=\dfrac{169}{4}\)

\(\Leftrightarrow\left[{}\begin{matrix}t+\dfrac{3}{2}=\dfrac{13}{2}\\t+\dfrac{3}{2}=-\dfrac{13}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{13}{2}-\dfrac{3}{2}=\dfrac{10}{2}=5\\t=-\dfrac{13}{2}-\dfrac{3}{2}=-\dfrac{16}{2}=-8\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+6x+5=5\\x^2+6x+5=-8\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+6x=0\\x^2+6x+13=0\end{matrix}\right.\)

Mà: \(x^2+6x+13=x^2+2.x.3+9+4=\left(x+3\right)^2+4\ne0\)

=> x² + 6x = 0

<=> x. (x + 6) = 0

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+6=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)

Vậy S = {0; -6}

a) Ta có: \(x^2+2x=\left(x-2\right)\cdot3x\)

\(\Leftrightarrow x\left(x+2\right)-3x\left(x-2\right)=0\)

\(\Leftrightarrow x\left[\left(x+2\right)-3\left(x-2\right)\right]=0\)

\(\Leftrightarrow x\left(x+2-3x+6\right)=0\)

\(\Leftrightarrow x\left(-2x+8\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\-2x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\-2x=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)

Vậy: S={0;4}

b) Ta có: \(x^3+x^2-x-1=0\)

\(\Leftrightarrow x^2\left(x+1\right)-\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\cdot\left(x^2-1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\cdot\left(x-1\right)\cdot\left(x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)

Vậy: S={-1;1}

c) Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)

\(\Leftrightarrow\left(x+1\right)\left(x+5\right)\left(x+2\right)\left(x+4\right)-40=0\)

\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)-40=0\)

\(\Leftrightarrow\left(x^2+6x\right)^2+13\left(x^2+6x\right)+40-40=0\)

\(\Leftrightarrow\left(x^2+6x\right)^2+13\left(x^2+6x\right)=0\)

\(\Leftrightarrow\left(x^2+6x\right)\left(x^2+6x+13\right)=0\)

\(\Leftrightarrow x\left(x+6\right)\left(x^2+6x+13\right)=0\)

mà \(x^2+6x+13>0\forall x\)

nên \(x\left(x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)

Vậy: S={0;-6}

minh biet

ta có : 

\(\left|x+1\right|+\left|x-1\right|=1+\left|\left(x-1\right)\left(x+1\right)\right|\)

\(\Leftrightarrow\left|x-1\right|\left|x+1\right|-\left|x-1\right|-\left|x+1\right|+1=0\)

\(\Leftrightarrow\left(\left|x-1\right|-1\right)\left(\left|x+1\right|-1\right)=0\Leftrightarrow\orbr{\begin{cases}\left|x-1\right|=1\\\left|x+1\right|=1\end{cases}}\)

\(\Leftrightarrow x\in\left\{-2,0,2\right\}\)

chuyển toán lớp 8 thành toán lớp 1 đi rồi giải cho ?

\(\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)=40\)

Đặt \(x+3=t\) Phương trình tương đương với

\(\left(t-2\right)\left(t-1\right)t\left(t+1\right)\left(t+2\right)=40\)

\(\Leftrightarrow\left(t^2-1\right)\left(t^2-4\right)t=40\)

\(\Leftrightarrow\left(t^4-5t^2+4\right)t=40\)

\(\Leftrightarrow t^5-5t^3+4t-40=0\)

Số xấu,không trình bày tại đây

a) \(\frac{x-45}{55}+\frac{x-47}{53}=\frac{x-55}{45}+\frac{x-53}{47}\)

\(\Leftrightarrow\left(\frac{x-45}{55}-1\right)+\left(\frac{x-47}{53}-1\right)=\left(\frac{x-55}{45}-1\right)+\left(\frac{x-53}{47}-1\right)\)

\(\Leftrightarrow\frac{x-100}{55}+\frac{x-100}{53}=\frac{x-100}{45}+\frac{x-100}{47}\)

\(\Leftrightarrow\frac{x-100}{55}+\frac{x-100}{53}-\frac{x-100}{45}-\frac{x-100}{47}=0\)

\(\Leftrightarrow\left(x-100\right)\left(\frac{1}{55}+\frac{1}{53}-\frac{1}{45}-\frac{1}{47}\right)=0\)

Vì \(\hept{\begin{cases}\frac{1}{55}< \frac{1}{45}\\\frac{1}{53}< \frac{1}{47}\end{cases}}\Rightarrow\frac{1}{55}+\frac{1}{53}-\frac{1}{45}-\frac{1}{47}< 0\)

\(\Rightarrow x-100=0\Rightarrow x=100\)

Vậy x = 100

Các phần sau tương tự nhé bạn