P(x) = 1+x+x^3+x^5+...+x^199+x^201
Tính giá trị P(x) tại x=1;x=-1
Bài 1: Tính giá trị của biểu thữ A với x = 999
A = x6 - x5 ( x - 1) - x4 ( x + 1) + x3 ( x - 1) + x2 ( x + 1) - x ( x + 1) +1
Bài 2: Rút gọn và tính giá trị của biểu thức.
a. 3x ( x - 4y ) - \(\dfrac{12}{5}\)y ( y - 5x ) ; Tại x = 4, y = - 5
b. 2u ( 1 + u - v ) - v ( 1 - 2u + v ) ; Tại u = -\(\dfrac{1}{3}\) , v = \(\dfrac{-2}{3}\)
Bài 2:
a.
\(3x(x-4y)-\frac{12}{5}y(y-5x)=3x^2-12xy-\frac{12}{5}y^2+12xy\)
\(=3x^2-\frac{12}{5}y^2=3.4^2-\frac{12}{5}.(-5)^2=-12\)
b.
\(u=\frac{-1}{3}; v=\frac{-2}{3}\Rightarrow u+v+1=0\)
\(2u(1+u-v)-v(1-2u+v)=2u(1+u+v-2v)+v(1+u+v-3u)\)
\(=2u.(-2v)+v(-3u)=-4uv-3uv=-7uv=-7.\frac{-1}{3}.\frac{-2}{3}=\frac{-14}{9}\)
Bài 1:
\(A=x^6-(x^6-x^5)-(x^5+x^4)+(x^4-x^3)+(x^3+x^2)-(x^2+x)+1\)
\(=-x+1=-(x-1)=-(999-1)=-998\)
Giá trị của đa thức x + x 3 + x 5 + . . . + x 99 tại x = -1 là
A. -100
B. -101
C. -51
D. -50
Tại x = -1 , thay vào đa thức ta được
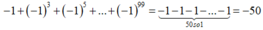
Chọn đáp án D
Bài 1: Tính giá trị của biểu thức.
a. A = x3-30x2-31x + 1 tại x = 31
b. B = x5-15x4+ 16x3-29x2+ 13x tại x = 14
c. C = x4 - 17x3 + 17x2 - 17x + 20 tại x = 16
d. D = x10 - 13x9 + 13x8 - 13x7 +...+ 13x2 - 13x + 10 tại x = 12
a: Ta có: x=31
nên x-1=30
Ta có: \(A=x^3-30x^2-31x+1\)
\(=x^3-x^2\left(x-1\right)-x^2+1\)
\(=x^3-x^3+x^2-x^2+1\)
=1
c: Ta có: x=16
nên x+1=17
Ta có: \(C=x^4-17x^3+17x^2-17x+20\)
\(=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+20\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+20\)
\(=20-x=4\)
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=10-x\)
=-2
Bài 1: Tính giá trị của biểu thức.
a. A = x3-30x2-31x + 1 tại x = 31
b. B = x5-15x4+ 16x3-29x2+ 13x tại x = 14
c. C = x4 - 17x3 + 17x2 - 17x + 20 tại x = 16
d. D = x10 - 13x9 + 13x8 - 13x7 +...+ 13x2 - 13x + 10 tại x = 12
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...+x^3+x^2-x^2-x+1+9\)
\(=-x+10=-2\)
bài 4 : phân tích đa thức thành nhân tử rồi tính giá trị của các biểu thức sau :
a, A= 4(x - 2) (x+1) + (2x - 4)2 +(x+1)2 tại x = \(\dfrac{1}{2}\)
b, B= x9 - x7 - x6 - x5 + x4 + x3 + x2 - 1 tại x=1
a,
\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)
Thay $x=\dfrac12$ vào $A$, ta được:
\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)
Vậy $A=\dfrac94$ khi $x=\dfrac12$.
b,
\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)
Thay $x=1$ vào $B$, ta được:
\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)
Vậy $B=0$ khi $x=1$.
$Toru$
Câu 6: Giá trị của biểu thức (x2 - 8) x (x + 3) - (x - 2) x (x + 5) tại x=-3là:
A.-4 B.16 C. -10 D. 10
Câu 7:Giá trị của biểu thức 6 + (x5 - 3) x (x3 + 2) - x8 - 2x5 tại x= -1/3 là:
A. -1/9 B. 1/9 C.9 D.-9
Câu 6: Giá trị của biểu thức (x2 - 8) x (x + 3) - (x - 2) x (x + 5) tại x=-3là:
A.-4 B.16 C. -10 D. 10
Câu 7:Giá trị của biểu thức 6 + (x5 - 3) x (x3 + 2) - x8 - 2x5 tại x= -1/3 là:
A. -1/9 B. 1/9 C.9 D.-9
câu 6 D
câu 7 A
Bài 1: Tính giá trị của biểu thức: x5 - 2009x4 + 2009x3 - 2009x2 + 2009x - 2010 tại x = 2008
Bài 2: Tính giá trị biểu thức 2x5 - 5x3 + 4 tại x, y thỏa mãn: (x - 1)20 + (y + 2)30 = 0
Bài 3: Tìm các cặp số nguyên (x, y) sao cho 2x - 5y + 5xy = 14
Bài 4: Chứng minh rằng đa thức P(x) = x3 - x + 5 không có nghiệm nguyên
Help ._.
Giá trị của đa thức x + x3 + x5 + x7 + x9 + ...... + x101 tại x = -1 là:
(A) -101;
(B) -100;
(C) -51;
(D) -50
Hãy chọn phương án đúng.
Thay x = -1 vào biểu thức đã cho ta được:
(-1) + ( -1)3 + (-1)5 + (-1)7 +...+ (-1)101
= (-1) + (-1) + (-1) + (-1) +(- 1)+ ... + (-1) (51 số -1)
= -51.
Chọn đáp án C
cho đa thức :P(x)=1+3x5-4x2+x5+x3-x2+3x3
Q(x)=2x5-x2+4x5-x4+4x2-5x
a)Thu gọn và sắp sếp các hạng tử của đa thức theo lũy thừa tăng của biến
b) Tính P(x)+Q(x);P(x)-Q(x)
c)Tính giá trị của P(x)+Q(x)tại x=-1
d)Chứng tỏ rằng x=0 là nghiệm của đa thức Q(x) nhưng không phải là nghiệm của đa thức P(x)
giúp với ạ
cho đa thức :P(x)=1+3x5-4x2+x5+x3-x2+3x3
Q(x)=2x5-x2+4x5-x4+4x2-5x
a)Thu gọn và sắp sếp các hạng tử của đa thức theo lũy thừa tăng của biến
b) Tính P(x)+Q(x);P(x)-Q(x)
c)Tính giá trị của P(x)+Q(x)tại x=-1
d)Chứng tỏ rằng x=0 là nghiệm của đa thức Q(x) nhưng không phải là nghiệm của đa thức P(x)
a.\(P\left(x\right)=1+3x^5-4x^2+x^5+x^3-x^2+3x^3\)
\(=1-5x^2+4x^3+4x^5\)
\(Q\left(x\right)=2x^5-x^2+4x^5-x^4+4x^2-5x\)
\(=-5x+3x^2+3x^4+2x^5\)
b.\(P\left(x\right)+Q\left(x\right)=1-5x^2+4x^3+4x^5-5x+3x^2+3x^4+2x^5\)
\(=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(P\left(x\right)-Q\left(x\right)=1-5x^2+4x^3+4x^5+5x-3x^2-3x^4-2x^5\)
\(=2x^5-3x^4+4x^3-8x^2+5x+1\)
c.\(P\left(x\right)+Q\left(x\right)=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(x=-1\)
\(P\left(x\right)+Q\left(x\right)=6.\left(-1\right)^5+3.\left(-1\right)^4+4.\left(-1\right)^3-5.\left(-1\right)+1\)
\(=-6+3-4+5+1=-1\)
d.\(Q\left(0\right)=\)\(-5x+3x^2+3x^4+2x^5\)
\(=0\)
\(P\left(0\right)=\)\(1-5x^2+4x^3+4x^5\)
\(=1\)
Vậy x=0 ko là nghiệm của đa thức P(x)