Trong hệ tọa độ Oxy, cho ABC có tọa độ đỉnh \(A\left(a,a+3\right)\), B(4;5), C(-3;2). Gọi d là pt của đg cao tam giác ABC hạ từ A. Tìm a để d đi qua M(-1;6)
JE
Những câu hỏi liên quan
Trong hệ tọa độ Oxy ; cho tam giác ABC có A(-2 ; 2) : B(3 ; 5) và trọng tâm là gốc tọa độ O(0 ; 0). Tìm tọa độ đỉnh C? A. C(-1 ; - 7) B. C( 2 ; -2) C. C(-3 ; -3) D. (1 ; 7)
Đọc tiếp
Trong hệ tọa độ Oxy ; cho tam giác ABC có A(-2 ; 2) : B(3 ; 5) và trọng tâm là gốc tọa độ O(0 ; 0). Tìm tọa độ đỉnh C?
A. C(-1 ; - 7)
B. C( 2 ; -2)
C. C(-3 ; -3)
D. (1 ; 7)
Trong hệ tọa độ Oxy ; cho tam giác ABC có A(-2 ; 2) : B(3 ; 5) và trọng tâm là gốc tọa độ O(0 ; 0). Tìm tọa độ đỉnh C?
A. C(-1 ; - 7)
B. C( 2 ; -2)
C. C(-3 ; -3)
D. (1 ; 7)
Chọn A.
Gọi tọa độ điểm C( x ; y)
Vì O là trọng tâm tam giác ABC nên 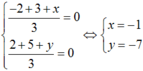
Đúng 1
Bình luận (0)
Trong mặt phẳng cho hệ tọa độ Oxy, cho tam giác ABC có đỉnh A(2; 2), B(1; -3), C(-2; 2). Điểm M thuộc trục tung sao cho \(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) nhỏ nhất có tung độ?
Gọi G là trọng tâm tam giác ABC
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{1}{3};y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{1}{3}\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|=\left|3\overrightarrow{MG}\right|=3MG\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\) nhỏ nhất khi \(3MG\) nhỏ nhất
\(\Leftrightarrow M\) là hình chiếu của \(G\) trên trục tung
\(\Leftrightarrow M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\le3MG=1\)
Đẳng thức xảy ra khi \(M\left(0;\dfrac{1}{3}\right)\)
\(\Rightarrow\) Tung độ \(y_M=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Trong hệ tọa độ Oxy, cho tam giác ABC có A(6; 1) ; B (-3; 5) và trọng tâm G(-1;1). Tìm tọa độ đỉnh C
A. ( 6 ; -3)
B. (- 6; 3)
C. (- 6; -3)
D. (- 3 ; 6)
Gọi C(x, y)
Vì G là trọng tâm tam giác ABC nên :
6 + − 3 + x 3 = − 1 1 + 5 + y 3 = 1 ⇔ x = − 6 y = − 3 .
Đáp án C
Đúng 0
Bình luận (0)
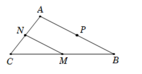
Trong hệ tọa độ Oxy, cho tam giác ABC có M(2; 3); N(0; -4); P(-1; 6) lần lượt là trung điểm của các cạnh BC; CA; AB. Tìm tọa độ đỉnh A?
A. A(1; 5)
B. A(-3; -1)
C. A(-2; -7)
D. A(1; -10)
Trong mặt phẳng với hệ tọa độ oxy , cho tam giác ABC có đỉnh A(4-1) phương trình đường cao và trung tuyến kẻ từ đỉnh B lần lượt là 2x-3y+12=0 và 3 và 2x-3y=0. Xác định tọa độ các đỉnh còn lại của tam giác ABC
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho tam giác ABC với \(A=\left(2;4\right);B=\left(1;3\right);C=\left(3;-1\right)\). Tính :
a) Tọa độ điểm D để tứ giác ABCD là hình bình hành
b) Tọa độ chân A' của đường cao vẽ từ đỉnh A
a)Gọi \(D\left(x;y\right)\) là tọa độ điểm cần tìm.
\(\overrightarrow{AD}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
Tứ giác ABCD là hình bình hành khi và chỉ khi:
\(\overrightarrow{AD}=\overrightarrow{BC}\)\(\Leftrightarrow\left\{{}\begin{matrix}x-2=2\\y-4=-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)\(\Rightarrow D\left(4;0\right)\).
b) Gọi\(A'\left(x;y\right)\) là điểm cần tìm. A' thỏa mãn hai điều sau:
- \(AA'\perp BC\). (1)
- A' , B, C thẳng hàng. (2)
\(\overrightarrow{AA'}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
\(\left(1\right)\Leftrightarrow\overrightarrow{AA'}.\overrightarrow{BC}=\overrightarrow{0}\)\(\Leftrightarrow2\left(x-2\right)-4\left(y-4\right)=0\) (3)
(2) suy ra hai véc tơ \(\overrightarrow{A'B}\) và \(\overrightarrow{BC}\) cùng phương.
Có \(\overrightarrow{A'B}\left(1-x;3-y\right)\).
Nên \(\dfrac{1-x}{2}=\dfrac{3-y}{4}\) (4)
Từ (3) và (4) suy ra: \(\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\).
Vậy A'(1;3).
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho hình bình hành ABCD có \(A\left(1;-2\right);B\left(3;2\right);C\left(-4;1\right)\). Tìm tọa độ đỉnh D ?
Gọi điểm D(x,y) là điểm cần tìm.
Tứ giác ABCD là hình bình hành khi và chỉ khi: \(\overrightarrow{AB}=\overrightarrow{DC}\).
\(\overrightarrow{AB}\left(2;4\right)\); \(\overrightarrow{DC}\left(-4-x;1-y\right)\).
\(\overrightarrow{AB}=\overrightarrow{DC}\)\(\Leftrightarrow\left\{{}\begin{matrix}-4-x=2\\1-y=4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-3\end{matrix}\right.\)\(\Leftrightarrow D\left(-6;-3\right)\).
Đúng 0
Bình luận (0)
cíu mình với :(
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có tọa độ các đỉnh A B C (1; 2) (3; -1) ; (4; 5 ). a. Tìm tọa độ các vectơ AB AC ; b. Tìm tọa độ trung điểm I của đoạn BC