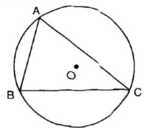
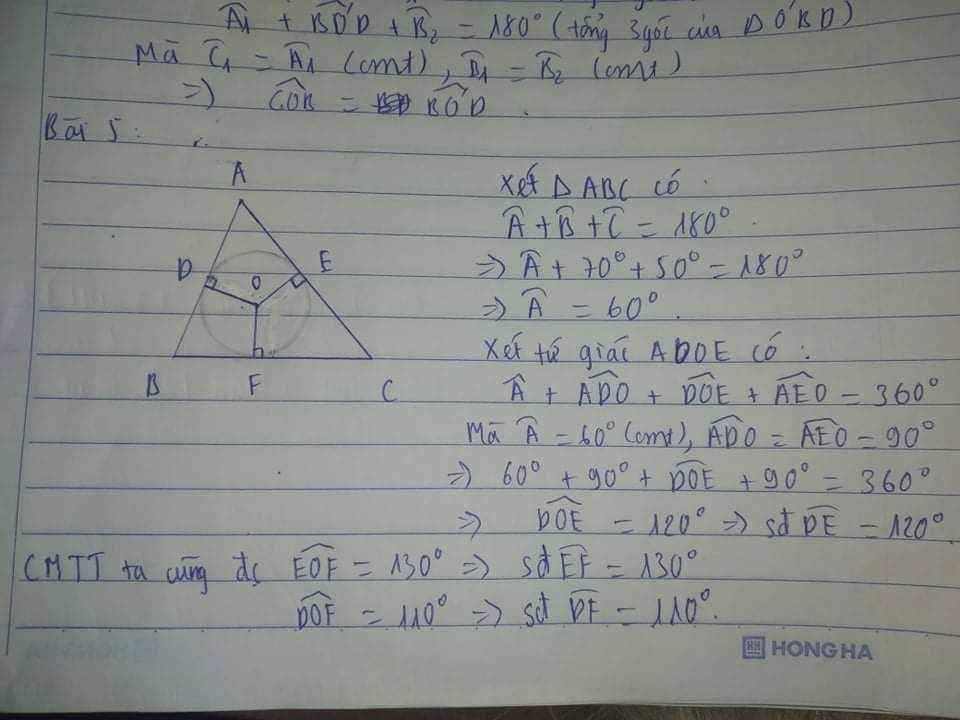Cho tam giác ABC nội tiếp đường tròn (O).Biết A=60°, B= 70°. Tìm số đo của các cung AB; BC; AC.
LS
Những câu hỏi liên quan
Cho tam giác ABC có B 70° ; C 50° nội tiếp trong đường tròn ( O ) .
a ) Tính số đo cung BC .
b ) Gọi AD , BE , CF lần lượt là các đường phân giác của các góc A , B , C . Tính : • Số đo các góc BEC , BED và FDE . • Số đo các cung CBF ; BCE . .
c ) Cho BC 6 cm . Tính bán kính đường tròn ( O ) .
Đọc tiếp
Cho tam giác ABC có B = 70° ; C = 50° nội tiếp trong đường tròn ( O ) .
a ) Tính số đo cung BC .
b ) Gọi AD , BE , CF lần lượt là các đường phân giác của các góc A , B , C . Tính : • Số đo các góc BEC , BED và FDE . • Số đo các cung CBF ; BCE . .
c ) Cho BC = 6 cm . Tính bán kính đường tròn ( O ) .
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là
x
+
75
0
,
2
x
+
25
0
,
3
x
-
22
°
. Một góc của tam giác ABC có số đo là:
(
A
)
57
°
5...
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75 0 , 2 x + 25 0 , 3 x - 22 ° . Một góc của tam giác ABC có số đo là:
( A ) 57 ° 5 ( B ) 59 ° ; ( C ) 61 ° ; ( D ) 60 °
Hãy chọn câu trả lời đúng.
Các cung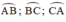 
tạo thành một đường tròn
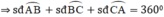
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
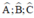là các góc nội tiếp chắn các cung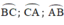 
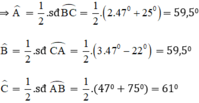
Vậy chọn đáp án C.
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là
x
+
75
0
,
2
x
+
25
0
,
3
x
−
22
0
. Một góc của tam giác ABC có số đo là:
(
A
)
57
°
5
;
(
B
)...
Đọc tiếp
Cho tam giác nhọn ABC nội tiếp đường tròn(O). Các cung nhỏ AB, BC, CA có số đo lần lượt là x + 75 0 , 2 x + 25 0 , 3 x − 22 0 . Một góc của tam giác ABC có số đo là:
( A ) 57 ° 5 ; ( B ) 59 ° ; ( C ) 61 ° ; ( D ) 60 °
Hãy chọn câu trả lời đúng.
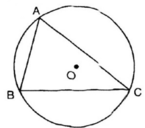
Các cung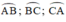 
tạo thành một đường tròn
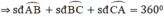
⇒ x + 75 ° + 2 x + 25 ° + 3 x − 22 ° = 360 ° ⇒ 6 x = 282 ° ⇒ x = 47 °
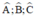là các góc nội tiếp chắn các cung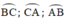 
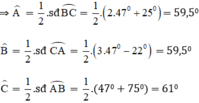
Vậy chọn đáp án C.
Đúng 0
Bình luận (0)
Cho tam giác ABC có B = 70°, C = 50°. Đường tròn (O) nội tiếp tam giác đó tiếp
xúc với các cạnh AB, BC, CA theo thứ tự tại D, E, F. Tính số đo các cung DE, EF và FD.
TD
Cho tam giác $ABC$ có $\hat{B}=70°$, $\hat{C}=50°$. Đường tròn tâm $O$ nội tiếp tam giác đó và tiếp xúc các cạnh $AB,$ $AC,$ $BC$ theo thứ tự $D,$ $E,$ $F$. Tính số đo các cung $DE,$ $EF$ và $FD$.
Xem thêm câu trả lời
cho tam giác ABC nội tiếp đường tròn (O) có góc A = 60 , B=50. so sánh các cạnh của tam giác ABC và các cung lớn AB,BC, AC
hjuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp đường tròn (O). Các cung nhỏ AB,BC,CA có số đo lần lượt là
x+10®, x+20®, x+30°. Tính số đo các góc của tam giác ABC.
Lời giải:
Ta có:
$x+10^0+x+20^0+x+30^0=360^0$
$\Rightarrow 3x+60^0=360^0$
$\RIghtarrow x=100^0$
$\widehat{ABC}=\frac{1}{2}\text{sđc(AC)}=\frac{1}{2}(x+30^0)=\frac{1}{2}(100^0+30^0)=65^0$
$\widehat{ACB}=\frac{1}{2}\text{sđc(AB)}=\frac{1}{2}(x+10^0)=\frac{1}{2}(100^0+10^0)=55^0$
$\widehat{BAC}=180^0-\widehat{ABC}-\widehat{ACB}=180^0-65^0-55^0=60^0$
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn với gốc B =60 độ nội tiếp đường tròn (O;5) và 2 đường cao BE,CF cặt nhau tại H a) CM AEHF và BFEC nội tiếp b) tính số đo cung nhỏ AC
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
b: \(sđ\stackrel\frown{AC}=2\cdot60^0=120^0\)
Đúng 1
Bình luận (0)
Bài 4: cho tam giác cân ABC nội tiếp đường tròn (O), cung nhỏ BC có số đo bằng 1000. Tia AO cắt cung nhỏ AC ở E.
a, Tính số đo các góc ở tâm BOE, COE
b, Tính số đo các cung nhỏ AB, AC.
