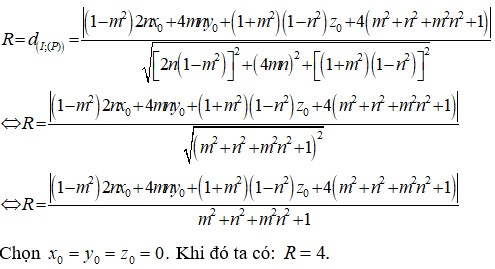m2-n2+10m+25
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PP
Những câu hỏi liên quan
a) m2 - n2 b) 4m2-16n2 c) 49 - 16x2 d) 25 - 9y2 e) 81x2-16y2
a, \(m^2-n^2=\left(m-n\right)\left(m+n\right)\)
b, \(4m^2-16n^2=\left(2m-4n\right)\left(2m+4n\right)=4\left(m-2n\right)\left(m+2n\right)\)
c, \(49-16x^2=\left(7-4x\right)\left(7+4x\right)\)
d, \(25-9y^2=\left(5-3y\right)\left(5+3y\right)\)
e, \(81x^2-16y^2=\left(9x-4y\right)\left(9x+4y\right)\)
Đúng 1
Bình luận (0)
Giải các phương trình sau: a)
3
m
m
+
1
−
3
x
−
2
0
khi
m
1
2
;b)
m
2...
Đọc tiếp
Giải các phương trình sau:
a) 3 m m + 1 − 3 x − 2 = 0 khi m = 1 2 ;
b) m 2 + 10 m + 25 x = m − 2 5 khi m = - 3 .
a) Tìm được x = - 1 b) Tìm được x = 17 20
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
(
P
)
:
(
1
-
m
2
)
2
n
x
+
4
m
n
y
+
(
1
+
m
2
)
(
1
-
n
2
)
z
+
4
(
m...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng ( P ) : ( 1 - m 2 ) 2 n x + 4 m n y + ( 1 + m 2 ) ( 1 - n 2 ) z + 4 ( m 2 + n 2 + m 2 n 2 + 1 ) = 0 Biết (P) luôn tiếp xúc với mặt cầu cố định. Khi đó bán kính mặt cầu cố định đó là:
A. 1
B. 2
C. 3
D. 4
Cho m, u là các số nguyên dương. Tìm giá trị chỏ nhất của vdk=m2+n2+1/m2+1/n2+2014
m2 + n2 + 2 ≥ 2 (m + n )
\(m^2+n^2+2\ge2\left(m+n\right)\\ \Leftrightarrow\left(m^2+2m+1\right)+\left(n^2+2n+1\right)\ge0\\ \Leftrightarrow\left(m+1\right)^2+\left(n+1\right)^2\ge0\forall m,n\)
Đúng 1
Bình luận (0)
m2 + n2 + 2 ≥ 2 (m + n )
⇔m2+n2+2-2m-2n≥0
⇔m2+n2+1+1-2m-2n≥0
⇔m2-2m+1+n2+2n+1≥0
⇔(m-1)2+(n-1)2≥0 (luôn đúng)
Đúng 1
Bình luận (0)
`m^2+n^2+2>=2(m+n)`
`<=>m^2+n^2+2>=2m+2n`
`<=>m^2+n^2+2-2m-2n>=0`
`<=>(m^2-2m+1)+(n^2-2n+1)>=0`
`<=>(m-1)^2+(n-1)^2>=0`
Ta thấy : `(m-1)^2>=0,∀m`
`(n-1)^2>=0,∀n`
`=>(m-1)^2+(n-1)^2>=0 \ ( ∀m,n)`
Đúng 0
Bình luận (0)
diện tích tam giác bên là: a 10 m2, b 5 m2 ,c 5m ,d 10m
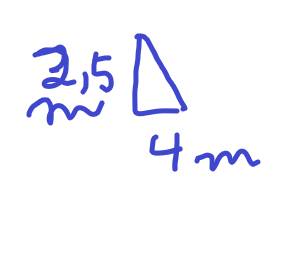
Xem thêm câu trả lời
m.n(m2-n2) chia hết cho 3
Nếu m hoặc n chia hết cho 3 thì hiển nhiên \(nm\left(m^2-n^2\right)⋮3\)
Nếu cả m và n đều không chia hết cho 3 thì \(m^2,n^2\) đều chia 3 dư 1 (tính chất của số chính phương). Do đó \(m^2-n^2⋮3\) nên \(mn\left(m^2-n^2\right)⋮3\)
Vậy \(mn\left(m^2-n^2\right)⋮3\) với mọi cặp số nguyên m, n.
Đúng 2
Bình luận (0)
Cho hình vẽ dưới đây biết a // (song song) b và widehat{M1} - widehat{N2} 50◦ Tính widehat{M2} và widehat{N2}
Đọc tiếp
Cho hình vẽ dưới đây biết a // (song song) b và \(\widehat{M1} - \widehat{N2}\) = 50◦
Tính \(\widehat{M2} và \widehat{N2}\)
Các thầy cô giúp dùm em với ạ
Cho 2 số không âm x, y thỏa mãn x2 + y2 x+y+xy. Biết rằng tập giá trị của biểu thức S x+ y là [m ; n]. Tính giá trị của biểu thức m2+n2
A. 16. B. 13 C. 25 D. 34
Đọc tiếp
Các thầy cô giúp dùm em với ạ
Cho 2 số không âm x, y thỏa mãn x2 + y2 = x+y+xy. Biết rằng tập giá trị của biểu thức S = x+ y là [m ; n]. Tính giá trị của biểu thức m2+n2
A. 16. B. 13 C. 25 D. 34
Ta có \(xy\le\dfrac{\left(x+y\right)^2}{4}\).
Do đó ta có: \(x+y+xy=x+y-2xy+3xy\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Rightarrow x^2+y^2\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Leftrightarrow\dfrac{1}{4}\left(x+y\right)^2-\left(x+y\right)\le0\)
\(\Leftrightarrow\left(x+y\right)\left[\dfrac{1}{4}\left(x+y\right)-1\right]\le0\)
\(\Leftrightarrow0\le x+y\le4\).
Do đó m = 0, n = 4.
Vậy m2 + n2 = 16. Chọn A.
Đúng 4
Bình luận (1)